认识数据
数据对象与属性类型
数据属性:通常是一个数据字段,也被称为“维”,“特征”,“变量”。分为:标称属性、二元属性、序数属性、数值属性(前三者定性,最后一个定量)
标称属性:用数表示所属类别、枚举;二元属性:0/1;序数属性:值与值间能反映一定的大小关系。中杯、大杯、超大杯
数值属性:分为区间标度属性和比率标度属性。后者有固定的零点,前者没有。温度采用℃时是区间标度,使用K时是比率标度。比率标度可以说x是y的多少倍,区间标度不行。
数据的基本统计描述
基础统计描述:
最大值、最小值
均值、加权平均
中位数
区间数据的中位数计算:
| 区间 | 频数 |
| a1-a2 | f1 |
| a2-a3 | f2 |
| … | … |
| an-an+1 | fn |
从上往下累加频数,计总频数为N。
找出中位数分布的区间,假设是ai-ai+1,则中位数为:
其中C为中位数所在区间之前的累计频数;h为区间宽度
众数(mode)
对于适度倾斜(非对称)的单峰数值数据,众数近似值计算:
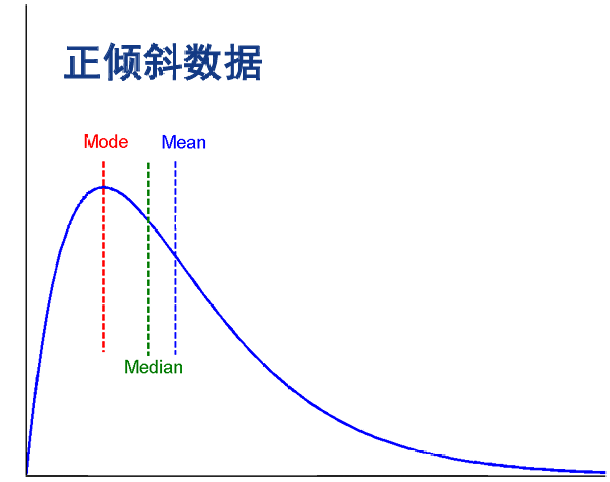
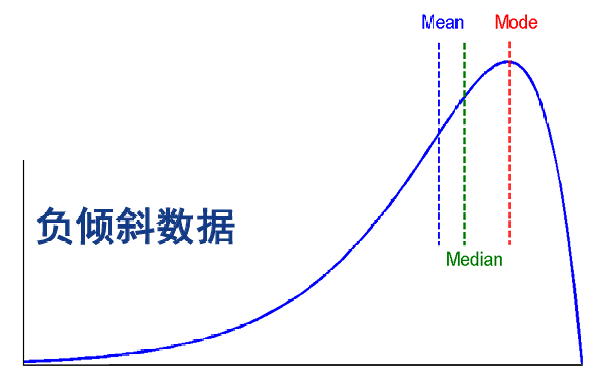
数据散布:
极差
分位数(2-分位数(中位数)、4-分位数(25%,50%,75%分位数))
中间四分位数极差IQR:75%分位数-25%分位数
孤立点:小于25%分位数-1.5*IQR或大于75%分位数+1.5*IQR的数据
五数概括:min,Q1(25%分位数),median,Q3(75%分位数),max
五数盒图:盒的三条线代表3个4-分位数,然后向上/下延伸到min/max,但延伸长度不超过1.5*IQR,以外的孤立点用点表示
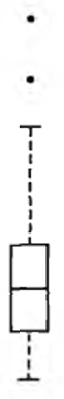
方差,标准差(方差的平方根)
数据的相似性和相异性度量
对象的相异性
数据矩阵:假设有N个对象,每个对象p个属性,则可以用n*p的矩阵存储所有数据
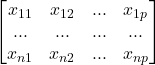
相异性矩阵:用一个n*n的上/下三角矩阵表示两个对象之间的相异性值(假设为d(i,j))。
同时可以定义相似度矩阵,值为sim(i,j)=1-d(i,j)
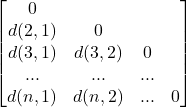
标称属性的相异性:
其中p是两个对象的属性个数,m是值相同的属性的个数
二元属性的相异性:
对于对象I和J,定义:
q 是对象I 和J都取1的属性数
r 是对象I 取1,对象J取0的属性数
s 是对象I 取0,对象J取1的属性数
t 是对象I 和J都取0的属性数

有时会认为负匹配t不重要(这种属性叫非对称二元属性),对应的相异性:
这种形式下的相似度也被称为Jaccard系数
数值属性的相异性,有多种方式度量:
- 欧氏距离(n=2时的闵可夫斯基距离)
- 曼哈顿距离(n=1时的闵可夫斯基距离)
- 闵可夫斯基距离(LP范数)
- 切比雪夫距离(n=+∞时的闵可夫斯基距离)
序数属性的相异性:
将属性值映射到[0,1]上,比如[中杯,大杯,超大杯]变成[0,0.5,1],然后按照数值属性进行相似度度量
如果数据中的属性值未能覆盖所有可能的属性值,也应该按照可能的属性值进行计算
比如目前有 优良中差 四种可能的取值:
如果数据中只出现了优良中,那么应该映射到{1,0.66,0.33};
如果数据中只出现了优良差,那么应该映射到{1,0.33,0};
以上情况只能用于属性类型一致的情况,如果属性是混合属性,则需要将上述四种方式结合。
设共包含p个属性:
对于其中的dij(f):
- 对于二元属性/标称属性,相等为0,相异为1
- 对于序数属性,映射到[0,1]然后当作数值属性
- 对于数值属性,映射到[0,1]然后计算
对于指示符δij(f):
如果两个值有任一个缺失,或者在该属性是非对称二元属性的前提下二者值均为0时,δij(f)=0;其余情况为1
例:
| 对象 | 属性1(标称) | 属性2(序数,可能取值包括优良中差),/为映射后 | 属性3(数值),/为映射后 |
| 1 | A | 优/1 | 45/0.55 |
| 2 | B | 中/0.33 | 22/0 |
| 3 | C | 良/0.67 | 64/1 |
| 4 | A | 优/1 | 28/0.14 |
属性1的相异矩阵:

属性2的相异性矩阵

属性3的相异性矩阵

由于并未出现缺值/非对称二元属性的情况,所以最终结果为三个矩阵对应位置取平均。

相似性度量
对非常长、稀疏的数据向量的相似性度量,可以计算余弦相似度,即:
数据预处理
数据清洗
缺失值处理
- 填入全局常量“unknown”
- 使用全局均值/中位数
- 用其他属性对客户进行分类,填写这个类内的均值中位数
- 使用回归、贝叶斯形式化、决策树等方法推理出一个值
噪声处理
分箱
通过考察数据的“近邻”(即周围的值)来光滑有序数据值
首先这些有序的值被分布到一些“箱”中;接着可以用箱均值光滑,用箱中位数光滑,用箱边界光滑
假设有一序列{4,8,15,21,21,24,25,28,34},先划分成(等深的)箱:{4,8,15}{21,21,24}{,25,28,34}
用均值光滑:{9,9,9}{22,22,22}{29,29,29}
用边界光滑:{4,4,15}{21,21,24}{25,25,34}(看中间值和哪个边界值更近,比如8和4更近,就替换成4)
回归
线性回归涉及找出拟合两个属性(或变量)的“最佳”直线,使得一个属性可以用来预测另一个
聚类
删除离群点
计算机和人工检查结合
略
数据集成
将数据从多个数据源合并到一致的存储
可能存在的问题:不同数据源中的相同实体如何识别;如何处理数据冗余
问题解决:
实体识别问题:
对于数据提前规定取值范围,以及处理空白、零或值的规则等,用来帮助避免模式集成的错误
注意不同数据源的表达方式不同
冗余问题:
使用相关分析检测:给定两个属性,度量一个属性能在多大程度上蕴涵另一个(标称属性,使用Χ2 (卡方)检验;数值属性,使用相关系数和协方差)
卡方检验
问题:性别(男/女)与是否喜欢某款游戏二者是否有关
| 性别 | 喜欢 | 不喜欢 | 总计 |
| 男 | 250 | 200 | 450 |
| 女 | 50 | 1000 | 1050 |
| 总计 | 300 | 1200 | 1500 |
1.计算期望值E\frac{行合计总计\times列合计总计}{总样本数} (请自行脑补latex)
对应的 男且喜欢;男且不喜欢;女且喜欢;女且不喜欢的E分别为:
然后根据卡方计算公式:
其中O是实际值,E是期望值
相关系数/皮尔森积矩系数
\bar{A}和\bar{B}是A和B的均值,σAσB分别是标准差
|rA,B|越接近1,相关性越强,越接近0越弱;rA,B>0说明正相关,反之负相关
以下省略一大堆
数据集成的方法:批量、增量、准实时、实时、事件、同步、异步、流处理、复制、归档
数据集成的架构:点对点、集中式、数据仓库、数据湖、服务导向、微服务、虚拟化、云化集成
数据规约
目标是将数据集缩小
方法:
- 维规约
- 小波变换(可能考简单计算,但是我看不懂一点)
- 主成分分析:属性与属性间可能存在一些线性关系,因此可以将多个变量线性组合成少数几个变量(考简单计算)
- 属性子集选择:通过某些原则(如决策树),去除掉作用较小的属性
- 数量规约
- 回归和对数-线性模型:用各种函数拟合属性间的关系
- 直方图(根据等宽/等深等方式分类), 聚类, 抽样
- 数据立方体聚集(将数据进行聚合,比如季度销量加和形成年销量,然后以年为尺度进行分析)
- 数据压缩:字符串压缩/音视频压缩
PCA主成分分析
以以下数据为例
A = [2.5, 2.4]
B = [0.4, 0.7]
C = [2.2, 2.9]
1.计算样本均值X及协方差矩阵S
定义协方差及协方差矩阵(以2维为例,若三维则为xyz),(n为样本数量)
在例子中:

2.解出协方差矩阵S的特征值λ,即|S-λI|=0的解
解二元一次方程得
进而得到与λ对应的特征向量(即Sv=λv)
特征向量满足如下式子:
需要设v=[x,y]然后解出x,y的比例,再归一化到单位长度
对于λ1:
解得
以上两个约等于是因为计算误差导致的,实际上会是一个值。
再进行归一化,v1=[0.713,-0.696]
对于λ2同理,v2=[0.696,0.713](因为是2维所以可以直接看出来,三维不行)
两个主成分的表示:
主成分的贡献度p:(经证明主成分的方差就是特征值大小)
对示例情况:
F1贡献度=0.06/(0.06+2.53)=0.02
F2贡献度=2.53/(0.06+2.53)=0.98
可以根据贡献度从大到小,对所有主成分进行排序,然后根据累计贡献度要求选出前几个主成分
数据变换与数据离散化
数据变换
通过变换将整个数据集的给定属性的值映射到新的值,每个老的值都能通过新的值识别
方法:
- 光滑Smoothing: 去除数据中的噪声(数据清理的方法);分箱、回归、聚类
- 属性构造Attribute/feature construction(数据规约方法)由给定的属性构造新的属性并添加到属性集中
- 聚集Aggregation: 对数据进行汇总,构造数据立方体(数据规约方法)
- 规范化Normalization: 把属性数据按比例缩放,使之落入特定大小区间;min-max normalization,z-score normalization,normalization by decimal scaling
规范化
最小-最大规范化min-max normalization
假设需要将[a,b]上的数据映射到[c,d],则
Z分数规范化
将连续的属性分割为有间隔的z-score normalization
定义μ为均值,σ为标准差,则
小数定标规范化normalization by decimal scaling
其中j是使max{|v’|}<1的最小整数,可以把全部数据映射到(-1,1)
离散化
典型方法:
- 分箱
- 直方图
- 聚类
- 决策树
- 相关分析
分箱
分箱可分为等宽分箱和等深/频分箱。前者最直观,但易受离群点影响,后者有良好的数据比例,但管理分类属性可能会非常棘手
假设有如下序列{4, 8, 9, 15, 21, 21, 24, 25, 26, 28, 29, 34}
等宽结果(宽为10):{4,8,9}{15,21,21}{24,25,26,28,29}{34}
等深结果(深为4):{4,8,9,15}{21,21,24,25}{26,28,29,34}
然后通过均值/中位数/边值光滑
分类(e.g.,决策树分析)
略
相关性分析
略
概念分层
使用高层次的概念替代低层次概念。比如青年,成年等替换年龄,使用省份替代城市
数据仓库与联机分析处理
数据指标体系设计与应用实践
以下省略一大堆
数据指标
数据指标按业务逻辑分成:北极星指标,结果指标,过程指标,运营指标,监控指标
按指标构成分成:原子指标,派生指标
好的数据指标的4个标准:1.简单易懂2.具有可比性3.是一个比率4.会改变行为
选择数据指标需要注意的4个问题:1.定性指标和定量指标都很重要2.警惕虚荣指标,选择可执行的指标3.先见性指标与后见性指标都很重要4.区分相关性指标和因果性指标
数据指标体系
三要素:极星指标(唯一关键指标)、核心指标、分析维度
数据指标会分为不同的层级结构,北极星指标是整个业务模块的核心指标,一级指标是北极星指标的下钻和拆解,而三级指标又是二级指标的下钻和拆解
为什么需要数据指标体系
1.形成标准化的衡量指标,监控业务发展状况
2.通过指标分级治理,快速定位业务问题,优化业务方向
3.形成标准化体系,减少重复工作,提高分析效率
数据指标体系构建的方法论
四个步骤
目标化,明确业务目标,梳理业务北极星指标
模块化及流程化,梳理业务流程,明确核心指标
层级化,数据指标分级下钻
维度化,维度选择实现数据指标的上卷下钻
4个步骤又涉及OSM、AARRR、UJM、MECE这4个模型,这4个模型是指导构建完整而清晰的数据指标体系的方法论
步骤实现方法简要概括
1.明确业务目标,梳理北极星指标
2.梳理业务流程,明确过程指标
3.指标下钻分级,构建多层级数据指标体
4.添加分析维度,构建完整的数据指标体系
数据埋点
数据埋点是用来记录和收集用户在使用产品时的各种操作行为
数据埋点设计的6个步骤
1.确认事件与变量
2.确认触发时机
3.确认上报机制
4.统一字段名
5.统一表结构
6.明确优先级
数据仓库
数据仓库的定义(不唯一):
一个提供决策支持功能的数据库,它与公司的操作数据库分开维护。为统一的历史数据分析提供坚实的平台,对信息处理提供支持
数据仓库是一个面向主题的、集成的、随时间而变化的、不容易丢失的
数据集合,支持管理部门的决策过程
数据仓库的特点:
面向主题:是数据仓库显著区别于关系数据库系统的一个特征
集成的:一个数据仓库是通过集成多个异种数据源来构造的
时变的(随时间而变化):数据仓库是从历史的角度提供信息,时间范围比操作数据库系统要长的多
非易失的:尽管数据仓库中的数据来自于操作数据库,但数据仓库总是在物理上分离保存的
操作型数据库主要支持OLTP联机事务处理,数据仓库主要支持OLAP联机分析处理
数据立方体
将多张二维表的数据合并成一个大立方体,可以是很多维
上卷:细粒度数据向高层合并
下钻:上卷的逆操作
切片:单独对某部分数据进行分析
转轴:“旋转”立方体,切换观察方向(实际效果是更换了二维表的行和列)
频繁模式挖掘及关联规则
支持度、置信度
假设我们有项集X={a,b}和项集Y={c},如何评价二者的关联程度?
支持度s:同时包含X和Y的数据的比例
置信度c:同时包含X和Y的数据占只包含X的数据的比例
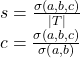
但是通过支持度、置信度的方法寻找频繁项集的方法非常暴力,在大范围数据上无法运算
优化:
1.任何由相同项(a,b,c)构成的X,Y的支持度是一样的,可以先判断支持度是否满足要求,再计算置信度
2.先验原理:如果一个项集是频繁的,则其子集必定频繁;如果一个项集是不频繁的,则其超集(自己是超集的子集)必定不频繁
频繁模式挖掘方法
Apriori:候选生成和测试方法
根据前面提到的第二条优化,如果一个项集是不频繁的,则其超集必定不频繁。所以从一项集开始计算,根据频繁一项集生成可能的频繁二项集(两个频繁项集取并集即可),直至找不到。
考虑下列数据,supmin=2,求频繁项集
| Tid | Items |
| 10 | A,C,D |
| 20 | B,C,E |
| 30 | A,B,C,E |
| 40 | B,E |
所有的一项集:{A}{B}{C}{D}{E},支持度计数分别为2,3,3,1,3;{D}不频繁
然后得出所有的候选二项集{A,B}{A,C}{A,E}{B,C}{B,E}{C,E},支持度计数分别为1,2,1,2,3,2;{A,B}{A,E}不频繁
进而得出所有的候选三项集{A,B,C}{A,B,E}{A,C,E}{B,C,E},支持度计数分别为1,1,1,2;{A,B,C}{A,B,E}{A,C,E}不频繁
最终得出所有频繁项集:{B,C,E}{A,C}{B,C}{B,E}{C,E}{A}{B}{C}{E}
提升Apriori的效率
Apriori的问题:
- 要对数据进行多次扫描;
- 会产生大量的候选项集;
- 对候选项集的支持度计算非常繁琐;
解决思路:
- 减少对数据的扫描次数;
- 缩小产生的候选项集;
- 改进对候选项集的支持度计算方法
改进方法1:哈希桶
再通过频繁n项集产生候选的n+1项集时,将n+1项集按哈希值进行散列,放入不同的桶中,可以直接根据最小支持度筛选部分数据
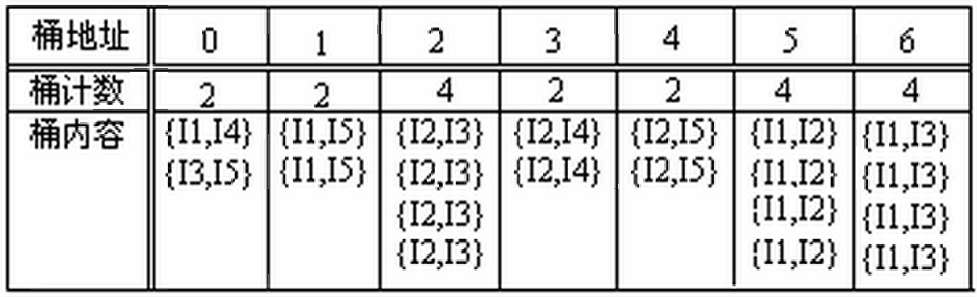
假设supmin=3,则0,1,3,4四个桶中的项集可以完全不考虑,但2,5,6中仍有可能有非频繁项集
改进方法2:划分
D中的任何频繁项集必须作为局部频繁项集至少出现在一个部分中,所以可以对数据集进行划分。第一次扫描:将数据划分为多个部分并找到局部频繁项集;第二次扫描:评估每个候选项集的实际支持度,以确定全局频繁项集
改进方法3:选样
选择一部分样本进行挖掘,可以通过适当降低最小支持度来减少遗漏的频繁项集
改进方法4:事务压缩
不包含任何频繁k项集的事务不可能包含任何频繁(k+1)项集,这种事务在下一步的计算中可以加上标记或删除
改进方法5:动态项集计数
在下图中,当我们发现{A,D}是频繁的,则立刻开始计算{A,B,D},如果发现{A,B,D}是频繁的,则说明{A,B}、{B,D}是频繁的
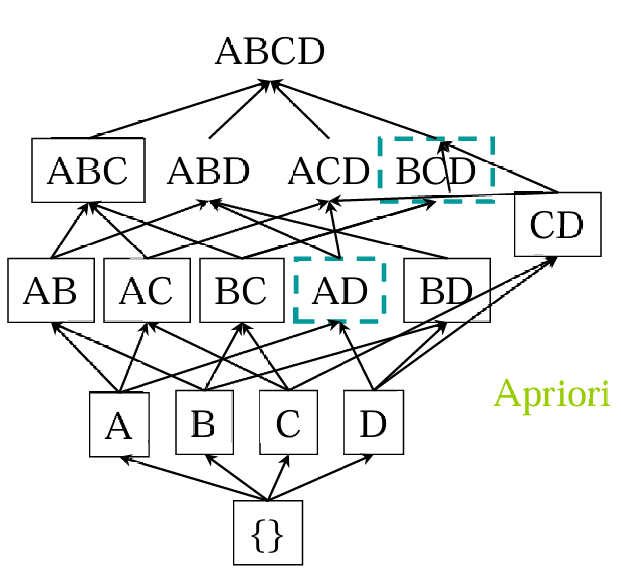
FPGrowth频繁模式增长
Apriori是广度优先搜索,可能产生大量频繁项集
FPGrowth是深度优先搜索,避免显式地产生候选
假设我们有如下事务
| TID | Items |
| 1 | {A,B} |
| 2 | {B,C,D} |
| 3 | {A,C,D,E} |
| 4 | {A,D,E} |
| 5 | {A,B,C} |
| 6 | {A,B,C,D} |
| 7 | {A} |
| 8 | {A,B,C} |
| 9 | {A,B,D} |
| 10 | {B,C,E} |
然后先对所有一项集计数,并按计数递减排列,得到
| TID | Count |
| A | 8 |
| B | 7 |
| C | 6 |
| D | 5 |
| E | 3 |
然后逐条遍历事务,按一项集计数递减的顺序排列节点,构造FPTree
读取TID=1的事务后
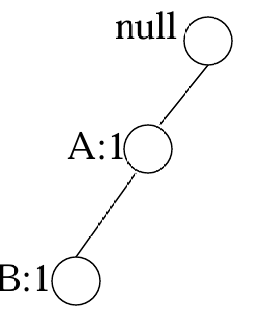
读取TID=2的事务后
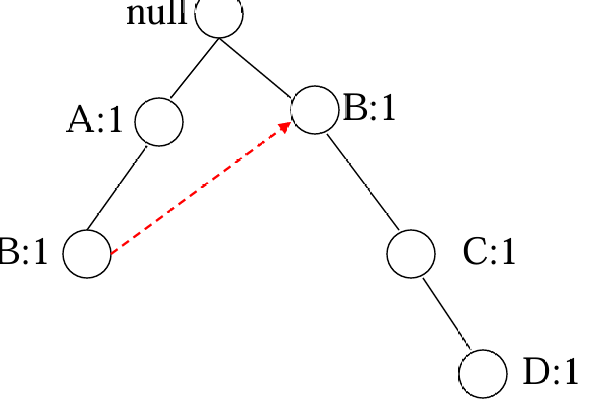
读取全部事务后:
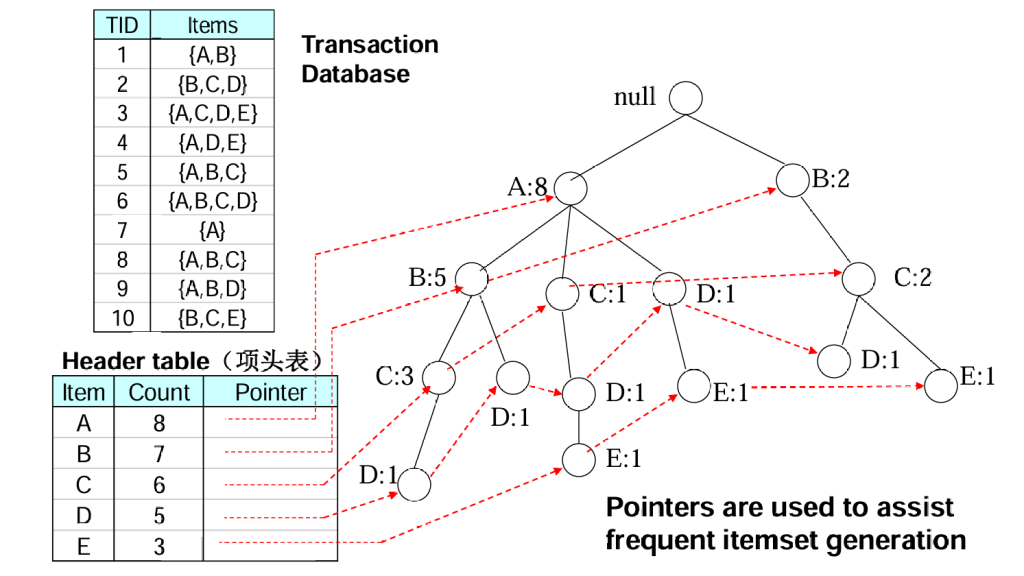
通常,FP树的大小比未压缩的数据小,因为购物篮数据的事务常常共享一些共同项
在最好情况下,所有的事务都具有相同的项集,FP树只包含一条结点路径
在最坏情况下,所有的事务都具有唯一项集,
同样也可以按支持度递增的顺序构造这棵FPTree,都不一定是最简单的FPTree
如何通过FPTree找到频繁项集:
首先分别找到以ABCDE结尾的频繁项集(通过虚线代表的指针)
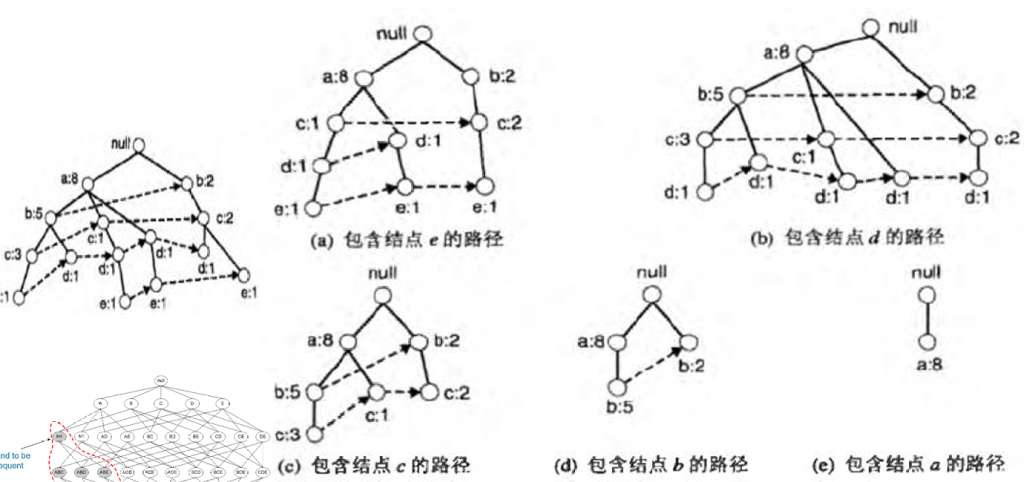
通过包含结点e的路径,我们可以得到以e结尾的前缀路径
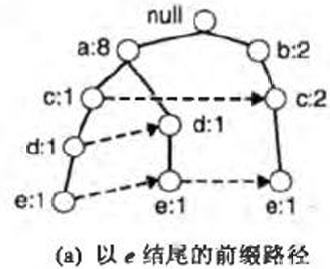
假设最小支持度为2,那么{e}是频繁项集,我们必须发现以de、ce、be、ae结尾的频繁项集。在解决这些子问题前,我们先通过以e结尾的前缀路径得到e的条件FP树
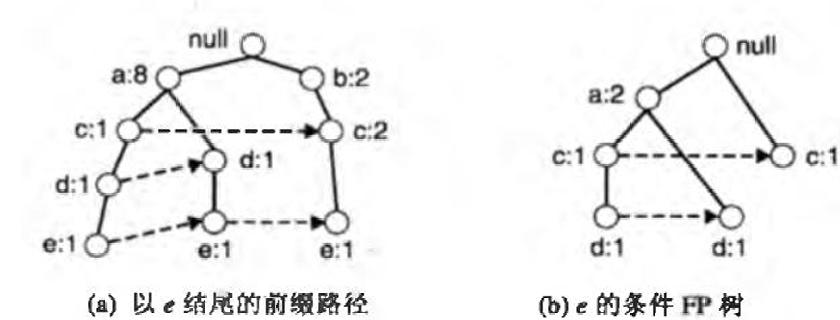
为了找到以de结尾的所有前缀路径,我们在e的条件FP树上,找到de的前缀路径
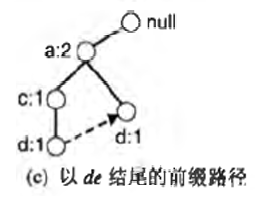
通过d的计数,可以得到{de}是频繁项集,于是我们可以计算下一个子问题:{ade}和{cde}是不是频繁项集,因为de条件FP树只包含一个支持度等于最小支持度的项A,所以我们不用再考虑cde了
步骤总结:
1.首先找出所有一项集,并筛选出频繁一项集
2.收集所有频繁一项集的前缀路径,这里不更新支持度
3.解决以频繁一项集结尾的频繁项集子问题。假设我们解决以e结尾的de、ce、be、ae,则我们在以e结尾的前缀路径上构建出e的条件FP树,注意这里要更新支持度
4.通过新的FP树解决子问题(再找出一项集abcd,……)
如果内存中FP-tree放不下怎么办?
——数据库投影
•将一个数据库分成多个投影
•为每个投影构造FP-tree并挖掘
关联规则的评估
以上方法挖掘出的规则可能是不符合实际逻辑的,可能产生误导,因此需要对频繁项集引入新的评价标准。以 使用相关性度量来扩充关联规则的支持度-置信度框架 为例
1.第一种相关性度量:提升度lift
假设我们有以下情况
| 打篮球 | 不打篮球 | 总计 | |
| 吃谷物 | 2000 | 1750 | 3750 |
| 不吃谷物 | 1000 | 250 | 1250 |
| 总计 | 3000 | 2000 | 5000 |
虽然打篮球→吃谷物的支持度/置信度分别为0.4/0.67,但实际上吃谷物的学生占整体学生的75%,会产生误导。打篮球→不吃谷物(s=0.2,c=0.333)更加可信。
定义提升度lift

2.第二种相关性度量:卡方检验,前面讲过,略
分类
决策树分类
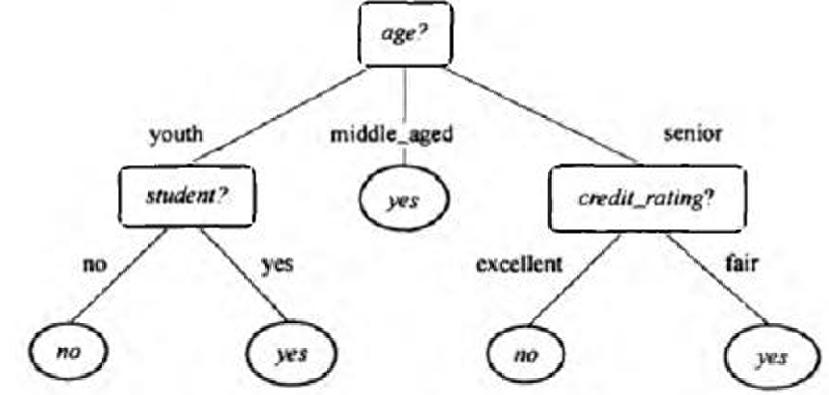
决策树的结构:
每个内部结点(非叶结点)表示在一个属性上的测试
每个分枝代表该测试的一个输出
每个叶结点存放一个类标号
树的最顶层结点是根结点
内部结点用矩形表示,而叶结点用椭圆(或圆角矩形)表示;
决策树可能是二叉树,也可能不是
决策树的构建有多种方法,只介绍一种最基础的HUNT算法。
Hunt 算法的基本思想:对于当前数据集 D,如果它已经“纯净”(即属于同一类别),则该节点为叶节点;否则,选择一个最优属性划分数据集,并对每个子集递归调用该算法。
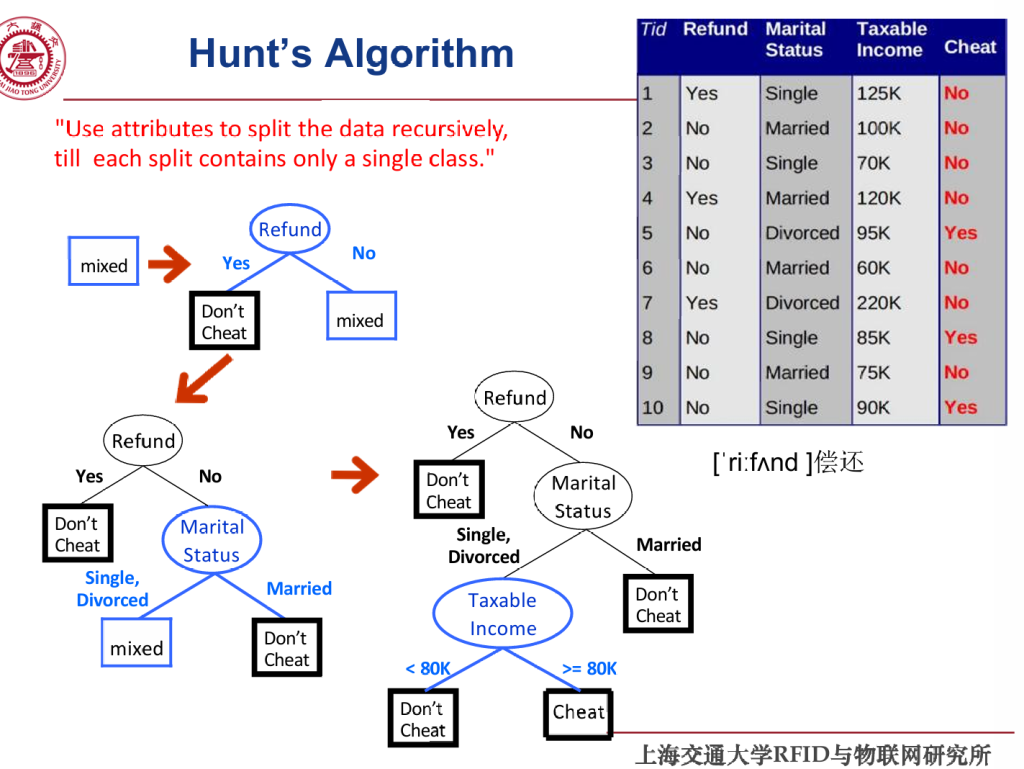
序数属性在划分时,如果需要将多个序数属性划在一个分支中,则必须保证多个分支间是有序的
计算”划分“的价值
基本想法:根据“划分”后的纯净(pure)度。节点越纯,说明并未进行有效的分类,所有数据仍分布在一侧。
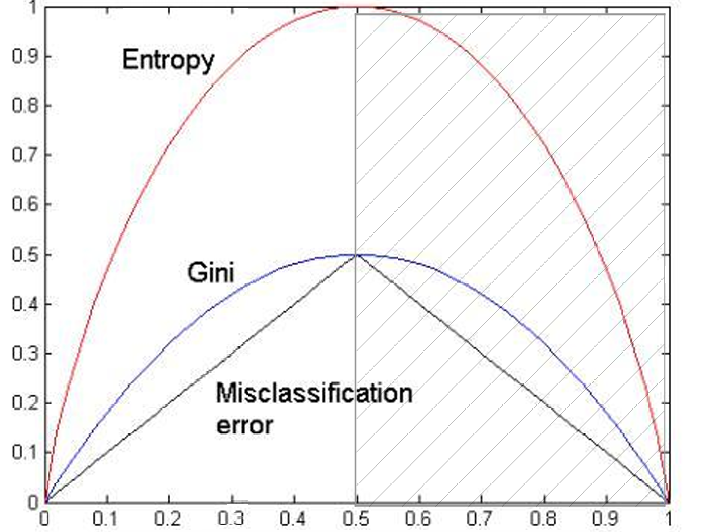
单结点的不纯性度量
一个单独节点的“杂乱程度“
方法:
- 基尼系数
- 熵
- 分类误差
在下面的计算种我们统一使用此例子:假设我们有10个样本,分类方法t1使得样本37开,t2使得样本55开
基尼系数
设t是分类回归树中的某个节点,k为当前属性下测试输出的类别数,p(j|t)为节点t中样本测试输出取类别j的概率
对节点t,G(t)越小,意味着该节点中所包含的样本越集中在某一类上,即该节点越纯,否则越不纯,差异性就越大。当节点t将样本平分到k个类中,基尼系数最大。
熵
假定S为样本集,t是分类回归树中的某个节点,k为当前属性下测试输出的类别数,p(j|t)为节点t中样本测试输出取类别j的概率,则该训练集S所包含的信息熵定义为
熵越小,说明节点约纯,。
分类误差
设t是分类回归树中的某个节点,k为当前属性下测试输出的类别树,p(i|t)为节点t中样本测试输出取类别i的概率
也就是说:CE = 不是多数类的样本占比
对节点t,CE越小,意味着该节点中所包含的样本越集中在某一类上,即该节点越纯,否则越不纯,差异性就越大。
子节点整体不纯度
父节点被划分后,所有子节点的不纯度加权平均
当我们根据某个特征划分节点后,会产生多个子节点 D1,D2,…,Dk,每个子节点也有各自的不纯度。
整体子节点不纯度是对这些子节点不纯度的加权平均:
假定我们希望将10个样本分类,目标为区分高/低收入(55开);我们首先按学历进行分类(节点D),其中高学历中收入4高2低(子节点D1),低学历中收入1高3低(子节点D2);则D的整体子节点不纯度为(假设我们使用CE作为不纯度指标(ppt里用的是熵)):
信息增益
定义为:用属性A划分样本集S,划分前样本数据集的不纯程度(熵)和划分后样本集的不纯程度(熵)的差值
假定属性A有k种不同取值,A将样本集划分成了S1,S2,…,Sk,则其中
信息增益越大,说明使用属性A划分后的样本子集越纯,越有利于分类
我们还使用按学历区分收入的例子:
增益率
基于以上,我们可以根据多种指标对一个“划分”进行评价,以及比较多个“划分”
模型评估
适用于决策树等多种分类模型
指标:错误率,用测试集跑一遍,略
真阳性TP:被分类器正确分类的正元组
真阴性TN:被分类器正确分类的负元组
假阳性FP:被错误地标记为正元组的负元组
假阴性FN:被错误地标记为负元组的正元组
混淆矩阵:
| actual/predict | C | ¬C | |
| C | TP | FN | P |
| ¬C | FP | FN | N |
| P’ | N’ | ALL |
准确率accuracy=(TP+TN)/ALL
错误率error rate=1-accuracy=(FP+FN)/ALL
灵敏度sensitivity=TP/P
特效性specificity=TN/N
精度precision=TP/(TP+FP)
召回率recall=TP/(TP+FN)
F度量及Fβ
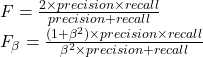
模型评估的方法:
- 保持方法:将数据集划分为训练集和测试集
- 交叉验证:将数据集划分为k个等大小的子集,然后轮流当测试集,其余做训练集,进行k次训练;每个子集恰好用于1次测试、(k—1) 次训练
超参数、模型比较,略
提高分类准确率的技术:
装袋:从训练集中有放回地抽取多个子集(每个子集大小和原始训练集一样,但含重复样本)。对每个子集分别训练一个模型。对于回归任务,使用平均法计算预测值;对于分类任务,使用投票法(多数投票)决定最终类别。
提升:给定训练集 D={(x1,y1),…,(xn,yn)}},初始时权重均为1/n,每轮训练结束后,提升错误样本的权重,然后归一化
随机森林:从原始数据集中进行有放回采样,生成多个子集(每个子集大小与原始集相同)。每个子集用于训练一棵决策树。在每个树的节点分裂时:并不是从所有特征中选择最优特征,而是从随机选出的部分特征中选择最优特征。最终所有树投票。
基于规则的分类
原理:通过给定规则给出分类结果
使用IF-THEN 规则分类
e.g.:IF (age=youth) AND (student=yes) THEN buys_computer=yes
令ncovers= 规则R 覆盖的元组数(满足前提的元组数)
ncorrect = 规则R 正确分类的元组数
覆盖率coverage(R) = ncovers /|D|
准确率accuracy(R) = ncorrect / ncovers
问题:多个规则间可能产生冲突(通过给定规则的优先级解决冲突);一些数据可能不满足任何规则(通过指定一个默认类解决)
IF-THEN 规则可以从决策树中提取而来
使用顺序覆盖算法的规则
通过一些算法,直接从训练数据中提取IF-THEN规则
贝叶斯分类、后向传播、支持向量机、惰性学习法
参照机器学习
频繁模式分类
关联分类
•关联规则由频繁模式产生并用于分类
•基本思想是可以搜索频繁模式(属性—值对的合取)与类标号之间的强关联
基于有区别力的频繁模式分类
•在构建分类模型时,频繁模式充当组合特征,可以看做是对单个特征的补充
其他分类方法
- 遗传算法:根据进化论,对初始种群进行筛选,通过遗传变异逐渐优化
- 模糊集方法:允许处理高层抽象;允许处理模糊或不精确的事实
- 粗糙集方法:把无法确认的个体都归属于边界线区域,而这种边界线区域被定义为上近似集和下近似集之差集。
集成学习法
将多个分类方法聚集在一起形成组合分类器,基于每个分类器投票得出结果
聚类
基于划分的方法
假设我们要将平面上的点划分到k个簇中,根据算法设计的知识,我们知道找到全局最优是一个NP问题,有两种启发式算法可以得到近似解。
- k-均值(k-means)算法
- k-中心点(k-medoids)算法
k-means算法
把簇的形心定义为簇内点的均值
给定k, k-均值算法由以下四步来完成:
- 随机的选择k个对象作为目前划分的簇的初始簇中心
- 对剩下的每个对象,计算与各簇中心的欧氏距离,将它分配到最相似的簇
- 使用上次迭代分配到该簇的对象,计算新的均值
- 使用新的均值作为新的簇中心,重新分配所有对象,直到分配稳定
优点:复杂度: O(tkn);其中n 是对象的数目, k 是簇的数目, t 是迭代的次数. 通常k、t << n
缺点:
- 需要事先给出k,簇的数目
- 对初始值选取敏感,常以局部最优结束
- 不能处理噪声数据和孤立点,对离群点敏感!
- 不适合发现非凸面形状的簇,或具有不同大小或密度的簇
- 只有在簇的平均值被定义的情况下才能使用,不能处理涉及有分类属性的数据(此时可以使用众数)
k-medoids算法
每一个簇用接近聚类中心的一个数据点表示
K-中心点是NP-hard问题,对小数据集很有效
- 从数据集中随机选择 K 个点作为初始 medoids。
- 将每个样本分配到距离最近的 medoid 所代表的簇。
- 尝试将 medoid 与簇中任意非 medoid 的点交换,看是否能降低总距离。如果能减少代价,就进行交换,直到无法再优化。
- 重复步骤 2 和 3,直到 medoids 不再变化或达到最大迭代次数。
基于分层、密度、网格的方法
略
推荐系统及社会网络
推荐系统
分类:基于内容/协同过滤
基于内容:尝试根据物品的内容(类型、颜色等)和用户的个人资料(喜好、人口统计信息等)将用户与物品进行匹配。
协同过滤:依赖于“相似用户喜欢相似物品”这一假设。推荐时会使用用户之间和/ 或物品之间的相似性度量来生成建议。
协同过滤的实现
首先建立效用矩阵,代表每个用户-物品对的评分
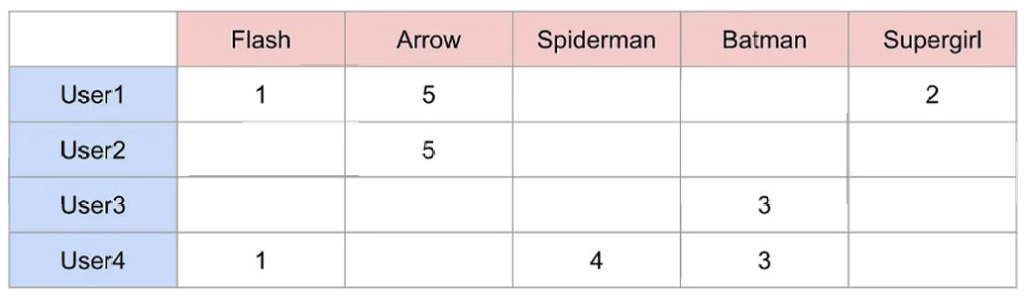
协同过滤的方法有user-user及item-item两种,此处以前者为例
对于用户x,通过相似度匹配(可使用余弦相似度等多种指标),找到N个与x行为相似的用户;
基于其他N个用户的行为,估计x对未交互物品i的评分。评分为与i交互过的k个用户对i的平均评分,或以相似度sxy为权重的加权平均
协同过滤的优缺点:
- 计算简单
- 可解释性好
- 大规模计算时效率低,存在较大空间复杂度
- 无法应对冷启动
推荐系统的评价指标
1.预测准确度:一般通过均方根误差RMSE/平均绝对误差MAE计算
2.Top-N 推荐:一般通过准确率(precision)/召回率(recall)度量。
数据集分为TP(true positive),FP(false positive),FN(false negative),
3.平均排名倒数:用于确定所找到的item是否被放在更明显的位置
4.累计增益CG、折扣累计增益DCG、标准化折扣累计增益NDCG
我们用以上三个指标衡量推荐列表中相关物品的位置对用户体验的影响。
假设我们有一个推荐列表,包含k个商品,对应的评分为r1-rk,CG为所有商品的评分加和
CG不受位置影响,只能反映k个商品的选取是否正确,为此我们引入DCG,使得前排商品更重要
DCG 的值本身不方便比较,需要标准化:使用理想排序的 DCG (IDCG)作为分母。
推荐系统的挑战:
- 长尾效应:热门物品样本较多,模型学习这部分的效果好,而冷门物品效果较差
- 流行度偏差:热门商品的推荐频率可能超过了它们的受欢迎程度,模型通常会给热门项目的评分高于其理想值,而不受欢迎的商品预测为负值;这种偏差会形成闭环并放大
- 稀疏性问题:当效用矩阵过大时,协同过滤方法失效,基于机器学习的模型容易产生过拟合
- 冷启动问题:新系统数据少,预测效果差
社会网络
社会网络也可以表示为一个矩阵,称为社会矩阵或邻接矩阵,对应的图一般是无向的;在一些社交媒体中,关注是单向的,此时社交网络是有向图
网络的直径是网络中最长的最短路径。如下图中2-9的最短路径是5,则直径是5
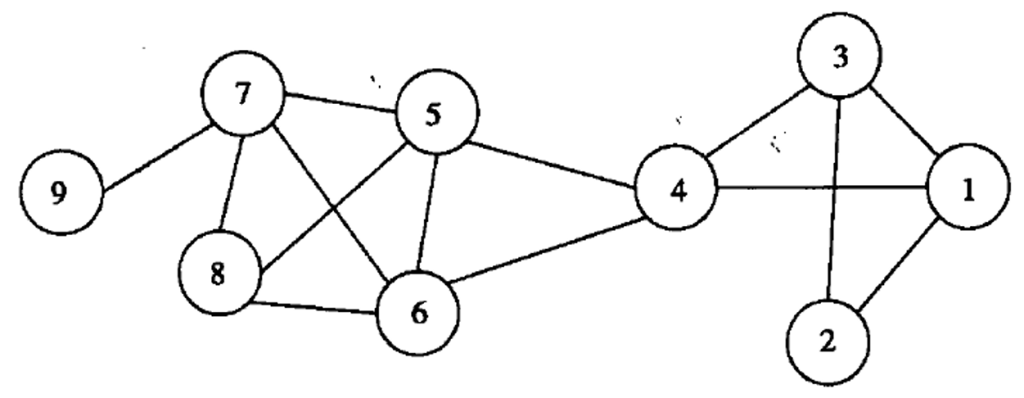
聚类系数:人们倾向于与一个团体中的人交往,与团体外的人交往较少。聚类系数表示:某个节点的邻居之间,有多少对彼此之间也有边。
- Ci:节点 i 的局部聚类系数
- ki:节点 i 的度(邻居个数)
- ei:在 i 的邻居之间实际存在的边的数目(即互相认识的朋友对数)
- ki(ki−1)/2:邻居之间理论最多可能连接的边数
- 若 ki<2,定义 Ci=0
社区发现
社区发现:识别一个结点的集合,使得集合内结点之间的相互作用比它们与集合外结点的相互作用更强
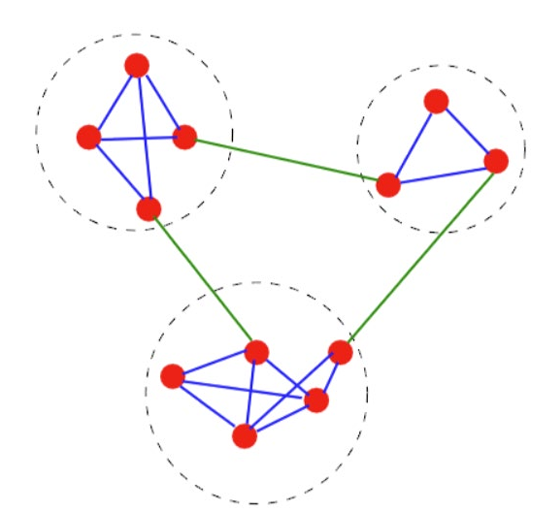
四类方法:
- 以节点为中心
- 以群组为中心
- 以网络为中心
- 以层次结构为中心
以节点为中心:目标是找出图中两两之间有边的顶点集合,即“团”。一般来说团越大则越有意义,但是最大团问题NP-hard。
团过滤算法CPM:
- 用户给定参数k,在网络中找出所有规模为k的团
- 如果两个团共享k-1个结点,那么将其合并
- 最终每一个连接的部分就是一个社区。
团过滤方法需要枚举所有给定规模为k的团,是一个NP-hard问题
以群组为中心:将一个群组内的所有链接(link)作为整体考虑,允许群组的某些结点具有低的连通性。比如当某顶点集合间的边数大于最大可能边数的90%,则将其算作社区。采取与团类似的策略进行求解。
以网络为中心:考虑网络的整体拓扑结构,目标是将网络的结点按照相似度划分为不相交的集合。
采用k-means算法或其他聚类算法即可,但是需要使用新的相似度度量,不能使用空间距离。
我们采用Jaccard系数或余弦相似度计算两个集合的相似度。
假设M={1,2,3,4}N={3,4,5,6};
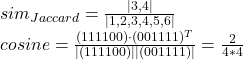
以层次为中心:分为分裂式层次聚类及聚合式层次聚类
分裂式层次聚类:
- 在每次迭代中,找到边介数最大的边,这类边很可能就是连接两个社区之间的边
- 删除那条边,然后更新各条边的边介数
- 一旦网络被划分为两个连接的部分,每一部分就认为是一个社区。重复以上过程就可以发现更小的社区
边介数的计算:网络中最短路径经过这条边的数量(如果最短路径有多种可选,那么将计数平摊)
聚合式层次聚类:
- 从基本的社区开始,按照某种标准不断将其聚合成更大的社区
- 如果两个社区的合并能够获得更高的整体模块度,那么就将其合并
- 开始时将每个结点视为一个社区,然后不断将他们合并
模块度计算:
- Q:整个网络划分的模块度
- m:图中的总边数
- 对每个社区 i:
- ei:社区 i 中的内部边的数量
- kCi:社区 i 中所有节点的度数之和
假设我们有如下社区分布:13个结点,23条边,分成3个社区
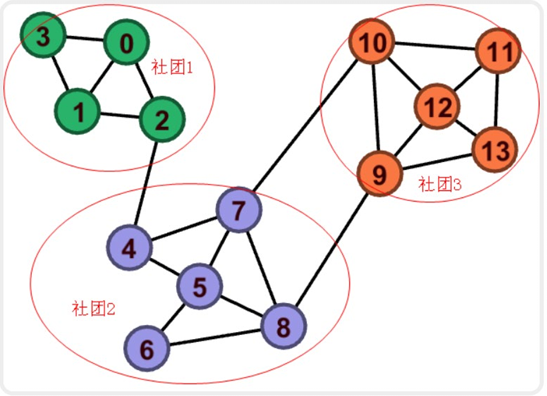

注意社团内的一条边会贡献两个度
社区发现的评估指标:熵、互信息、归一化互信息
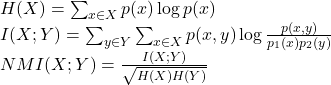
其中X为算法的划分结果,Y为真实划分;
还可以通过神经网络对图进行编码、特征学习等
Jiliokvip, heard good things about your JILI slots. Tried ’em out and they’re actually legit! Graphics are crisp and payouts seem fair. A little slow on withdrawals, though. Anyways, check it: jiliokvip.
Yo, just checked out vipjl777 and it’s pretty slick! Games are smooth, and the site’s easy to navigate. Might be my new go-to. Check it out for yourself! vipjl777
Jili77login, eh? Quick and easy to log in, which is a major plus. Games load fast, and I haven’t had any issues yet. Could be a winner! You gotta give it a shot. jili77login