关于考试
sigmoid便捷计算
- 1.输入1÷(1+e^-x) (e^在shift+LN;x在alpha+))
- 2.按 =
- 3.按CALC
- 4.输入x
- 5.连按两下=
- 6.重复3-5
y=sigmoid(x);则y’=y(1-y);δx=δy*y(1-y)
系统设计
一、监督学习(有标签数据)
回归任务(预测连续值):
- 线性回归 LR(简单)
- 多层感知机 MLP(复杂)
分类任务(预测离散标签):
- 逻辑回归 LR
- 决策树(Decision Tree)
- K-近邻 KNN
- 贝叶斯分类(Naive Bayes)
- 支持向量机 SVM
- 多层感知机 MLP
二、无监督学习(无标签数据)
聚类任务:
- 聚类(Clustering)(K-Means)
降维任务:
- 降维(Dimensionality Reduction)
- PCA主成分分析(线性)Autoencoder自编码器(非线性)
三、深度学习模型(以神经网络为基础)
神经网络结构:
- 卷积神经网络 CNN:主要用于图像识别(机器视觉)
- 多层感知机 MLP:基础神经网络,可用于多种任务
- Transformer:序列建模结构,广泛用于 NLP 和图像等任务
- 大语言模型 LLM:以 Transformer 为基础的预训练语言模型(如 GPT、BERT)
四、自然语言处理(NLP)相关
- Word2Vector:将自然语言转成词向量
- 语言模型:RNN、Transformer ,用于建模自然语言的概率分布
- Transformer:现代 NLP 的主力模型(如 BERT、GPT)
- 大语言模型 LLM:微调、参数化微调、提示词工程、RAG检索增加生成
- CNN:对词向量层层卷积,提取特征
五、生成式模型(Generative Models)
- 生成式模型:学习数据的分布以生成新样本,例如:
- 各种GAN(生成对抗网络)
- VAE(变分自编码器)
- 去噪扩散模型
六、强化学习(Reinforcement Learning)
- 强化学习 RL:Q-Learning及DQN
七、机器视觉
- 图片分割:卷积+逆卷积
- 物体识别=划分+分类;划分:fast/faster R-CNN
- 文图互转:视觉语言模型VLM
八、答题模板
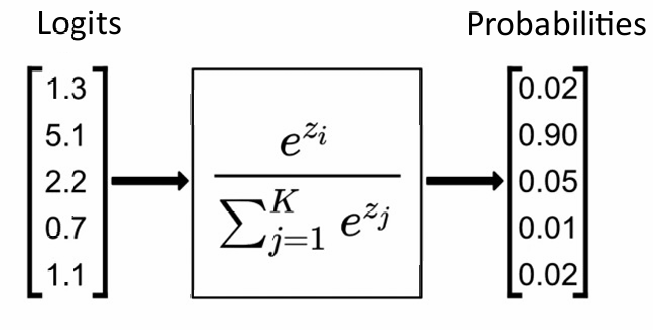
本系统旨在解决【任务描述,例如:图像中的人脸识别、文本情感分类、用户购买行为预测】问题。该问题可以视为一个【分类 / 回归 / 生成 / 强化学习】任务。
- 数据收集与预处理
首先采集包含【描述数据来源,例如:图片、文本、传感器数据等】的数据集,对数据进行清洗、缺失值处理、归一化(或分词、编码)等预处理操作,以便模型有效学习。 - 特征工程
提取并构造关键特征,如【示例特征,如:图像的边缘特征、文本的TF-IDF向量、用户行为统计特征等】,必要时进行降维以提高训练效率。 - 模型选择
选择适用于本任务的模型:如为分类任务,可选择逻辑回归、决策树、SVM、MLP等;如为回归任务,可选用线性回归、MLP、SVR;如为生成任务,可选用生成式模型(GAN、VAE)或大语言模型;如为决策控制任务,可使用强化学习(如Q-Learning、DQN等)。 - 训练与评估
使用训练集进行模型训练,采用交叉验证防止过拟合,并用验证集/测试集评估模型性能,指标包括准确率、F1分数、均方误差或累计奖励等。
Intro
泛化性与过拟合
学习的泛化性问题:模型应该学习普遍的规律还是记住特定细节
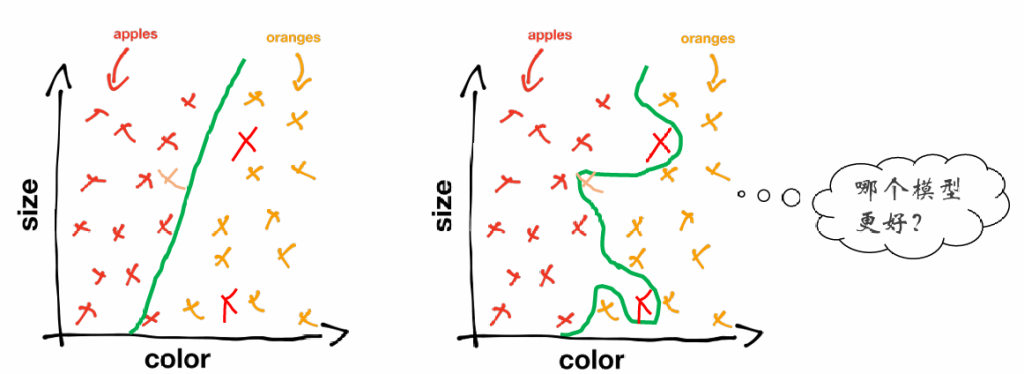
欠拟合–因模型不够复杂无法刻画真实规律,模型假设可能不成立
过拟合–因模型过于复杂导致记住数据的细节(如随机噪声)而不是潜在的规律
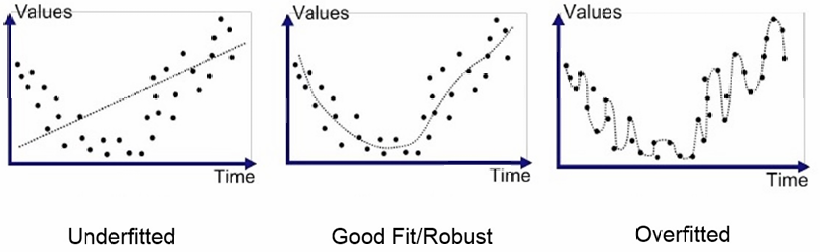
避免过拟合的方法:
- 增加训练数据
- 正则化(模型过于复杂时给予惩罚)
- 数据划分&交叉验证(训练时保留部分未知数据用于测试,以检验泛化能力)
- 早停
- 引入先验知识(如贝叶斯先验)
线性回归
用线性函数拟合数据,根据最小二乘法给出结果。
线性函数:
损失函数:
对于一个输入样本x,模型输出y,真实值r,则将平方误差定义为
对于完整数据集D={(x(1),r(1)),…,(x(n),r(n))}损失函数定义为均方误差MSE:
使用梯度下降法优化损失函数
优化目标:
迭代步骤:
其中
但是用梯度下降法求线性回归实际上走了弯路,因为线性回归可以用数学方法得出最优解。我们借助矩阵形式的线性回归来说明这个问题。令:
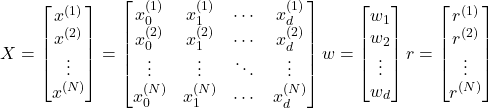
预测值:
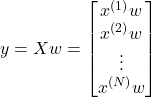
损失函数:
梯度:
最优参数w*:
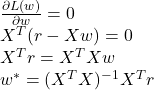
对应的最优线性函数为:
我们只需算出H即可
问题:XTX可能不可逆,导致我们还是只能使用梯度下降法
解决:使用正则化,对损失函数引入惩罚项
新的最优解:
XTX + λI一定是满秩的,所以一定可逆
决策树
分类问题中,我们可能遇到不线性可分的示例,或是属性值不是数字,但是沿某些维度局部线性可分
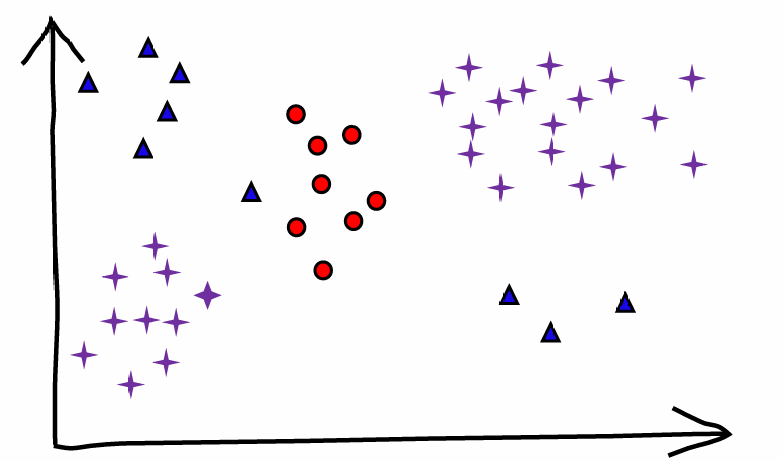
决策树的基本思想:分而治之
在小范围内按线性分类
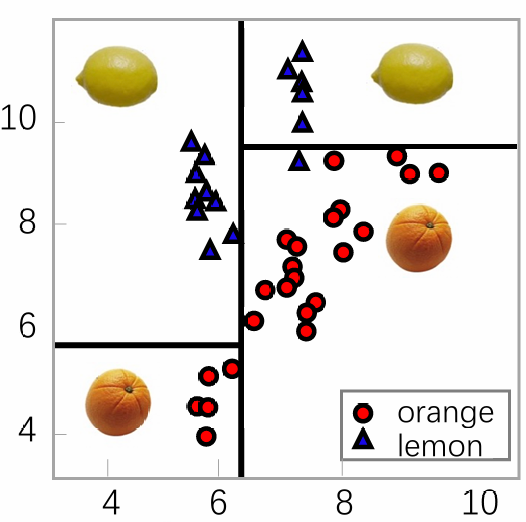
构造决策树的过程:
- 构造一个根节点,包含整个数据集
- 选择一个最合适的属性
- 根据选择属性的不同取值,将当前节点的样本划分成若干子集
- 对每个划分后的子集创建一个孩子节点,并将子集的数据传给该孩子节点
- 递归重复2~4直到满足停止条件
关键问题:
如何高效率的构建决策树?
——选择每个属性X的时候,尽可能最大化标签Y的纯度
如何选择属性以最大化标签的纯度?
——选择X以最大化信息增益、Gini系数等
ID3算法即根据信息增益进行划分
定义熵——刻画一个数据集合的不纯净度
假设数据集D中有K种不同的分类,定义为{C1,…,Ck},则:
假设我们选定属性A作为一个分类,属性A将D分成n类,定义为{D1,…,Dk},则:
信息增益定义为:
假定我们希望将10个样本分类,目标为区分高/低收入(55开);我们首先按学历进行分类(节点D),其中高学历中收入4高2低(子节点D1),低学历中收入1高3低(子节点D2):
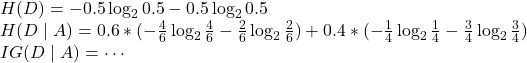
算法优缺点:
优点:
- 易理解, 可解释性, 便于可视化分析
- 数据预处理要求低
- 可以轻易处理非线性边界
- 数据驱动,可以以任意精度拟合训练集
缺点:容易过拟合(噪声样例也会被学习)
解决:
随机森林:将数据随机划分子集,各自构建决策树,按多个决策树的结果投票决定。
随机森林的优点:
- 往往比决策树更准确
- 训练速度快, 容易并行化 (训练时树与树之间是相互独立的)
- 可以处理高维(feature很多)数据,并且不用做特征选择 (因为特征子集是随机选择的)
- 可以处理缺失属性
- 结果易解释 (i.e.,在训练完后,能够给出哪些feature比较重要)
- 在训练过程中,能够检测到feature间的互相影响
- 对于不平衡的数据集来说,它可以平衡误差
贝叶斯分类
某些情况下,不同类型的数据交融在一起,决策树算法就无法准确区分
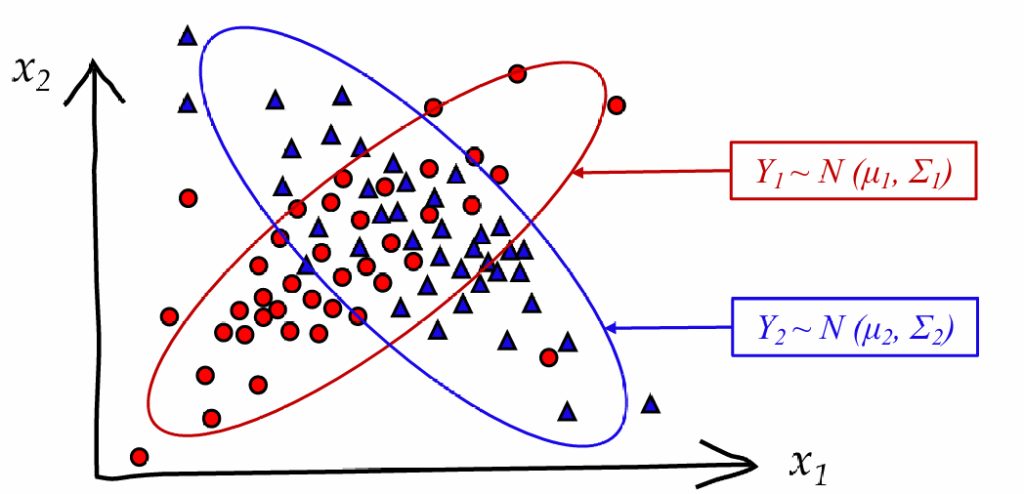
我们通过计算某个位置的点属于某一类的概率,来解决这个问题
贝叶斯公式:
P(Ci)先验概率:在没有观察到数据之前,我们对某个事件(如某个类别)的原始估计。表示我们在没有任何特征信息的情况下,一个样本属于类别Ci的可能性。
p(x | Ci)似然(likelihood):在类别为 Ci 的前提下,观察到特征 x 的概率;
p(x)证据(evidence):是所有类别下生成特征 x 的总概率,用于归一化。
P(Ci | x)后验概率:表示在观察到特征 x 后,样本属于类别 Ci 的概率
在复杂问题中,我们不只考虑一个特征x,因此上式会变为:
由于我们最终只关注概率的相对大小,而分母(evidence)是统一的,所以我们需要计算:
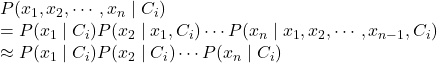
独立性假设(朴素贝叶斯假设):如果我们假设各个x间是独立的,则上面的约等于是成立的
贝叶斯分类的训练过程也就是计数,统计出所有的P(xj | Ci),有时可能出现值为0的情况,可以通过虚拟计数的方式:
优点:
- 训练、测试过程速度快
- 表现好:当独立性假设成立时,效果好;面对多分类问题也表现良好
- 易于在数据集更新时进行训练,算法易维护
缺点:
- 依赖于独立性假设
- 容易欠拟合
K-近邻 KNN
基本思想:根据距离自己最近的几个点的所属类别进行投票
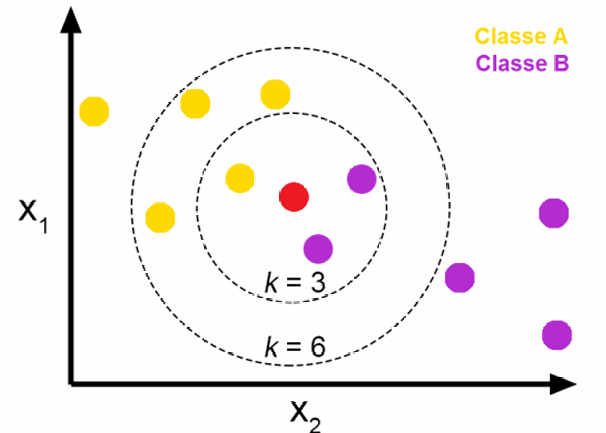
距离指标的选取:
- 欧氏距离(受维度影响较大)
- 曼哈顿距离
- 闵可夫斯基距离
由于各个属性的尺度不一定一致,因此需要对每个属性分别进行归一化
有时也不一定使用距离作为限制,使用相似度(比如余弦相似度)也可以
K的选取:
维诺图:
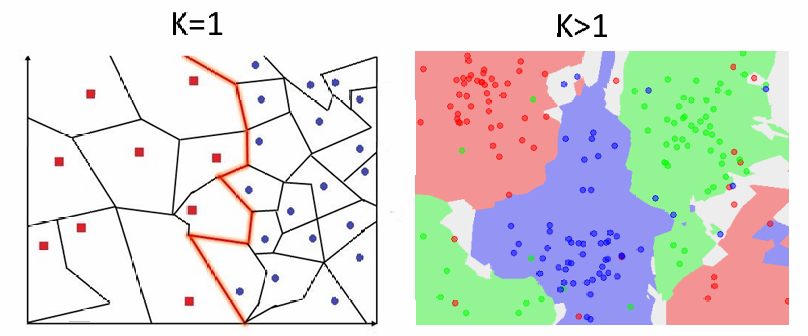
k越小:更能反映局部细节,但会导致过拟合
k越大:边界更加平滑,也可能导致欠拟合
优点:
- 易于理解、解释和实现
- 训练难度低
- 可以无缝添加新数据,而不会影响模型的准确性
缺点:
- 不适用于大型数据集(计算距离的计算成本很高)
- 极易受到维度的影响
- 需要大量存储
- 需要数据归一化
逻辑回归LR
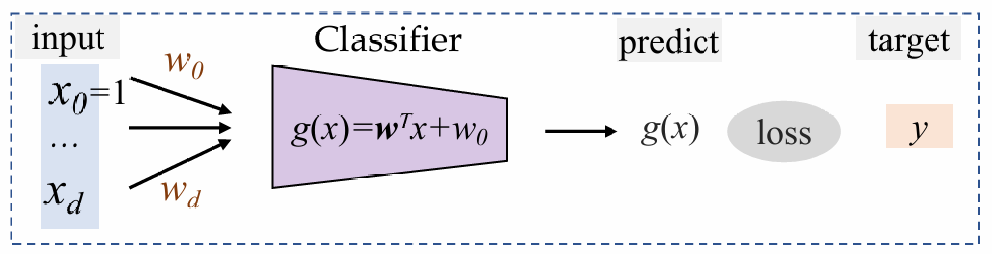
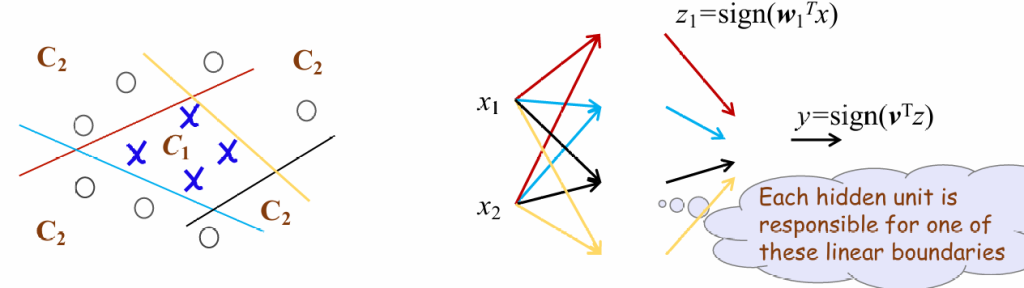
我们将上面三个算法归纳成:靠一个判别函数对空间进行划分。
我们将判别函数设置成线性函数,根据取值正负划分类别,函数值为0的位置是一个超平面,分割整个标签。
使用感知机
感知机的结构非常简单,其输出g(x)只有{1,0},根据判别函数的符号决定
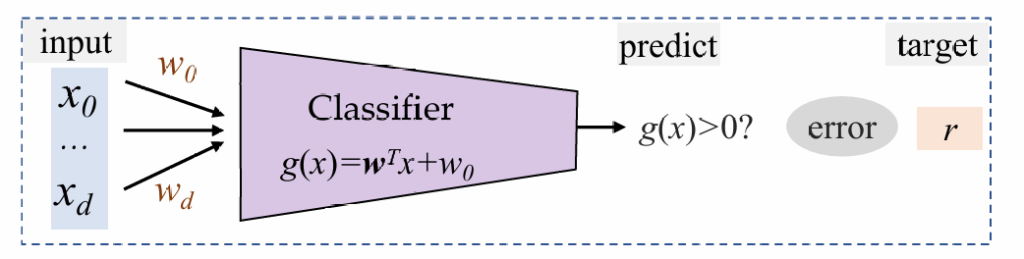
训练过程:
规定数据集D={(x(1),r(1)),...,x(d)r(d)};
for (x(l),r(l)) in D:
| if r(l)g(x(l))≤0:(预测与实际不一致)
| | w=w+ηr(l)x(l)(将超平面向被错误分类的点移动,η为学习率)
重复上述过程,直至全部数据集都被正确分类感知机的问题:
输出只有0和1,过于生硬,难以优化
使用sigmoid
我们首先定义y为数据点x属于类别C1的概率,相应的,属于C2的概率就是1-y,然后根据
是否大于零,来判断应该属于哪一类
如果数据满足正态分布,那么我们可以得到:(推导省略)
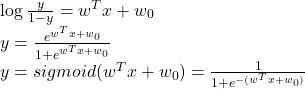
我们将损失函数定义为,或称为交叉熵损失CE:
最小化损失函数等价于最大化似然(likelihood)
训练过程:通过梯度下降法最小化损失函数
对于整个数据集D而言:
我们定义
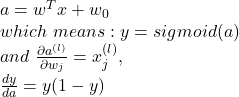
则有
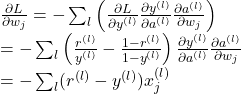
多分类问题
有时我们需要预测多个类,如果我们想统一处理所有类而不必选择参考类,我们可以使用 softmax 函数来代替后验类概率y
其中
交叉熵损失函数及梯度:
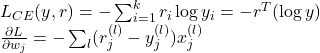
支持向量机SVM
先前的分类方法中,我们的目标只是得出一个正确的结果,结果和结果间的优劣怎么评价?
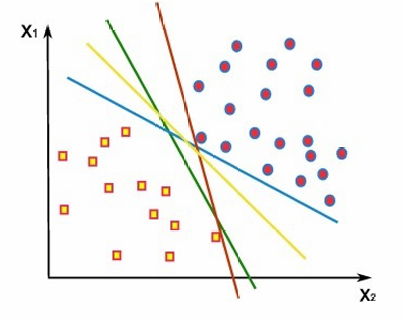
我们希望分割线距两边的间隔最大,我们定义两条虚线,间隔最大时两条虚线会刚好卡在两个类的边界下
间隔:
最大化margin等价于最小化0.5*||w||
写成一个优化问题的形式:
因为y的取值只有±1,所以保证了所有点在两条虚线外
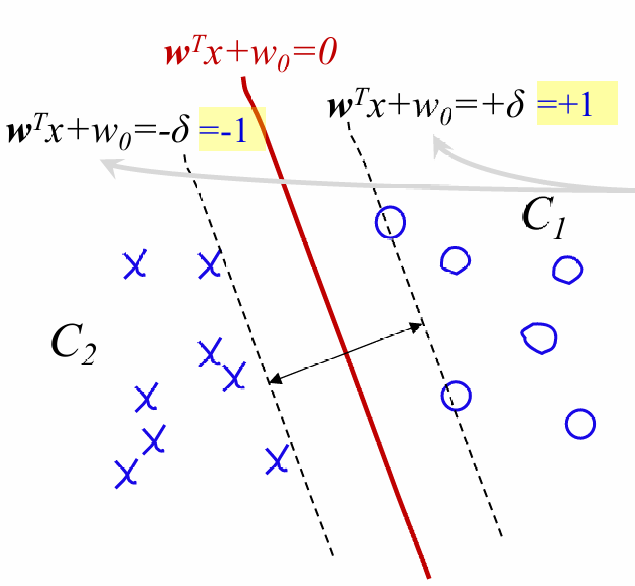
我们还是采用感知机作为模型:
损失函数:
我们首先希望y(wTx+w0)>1,所以我们需要优化其中最小的值,直至其大于1
当所有点都在虚线以外,我们开始调整w使虚线卡在边界上。
可以得出:
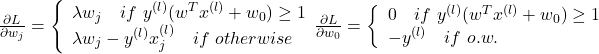
多层感知机MLP
根据人类的神经结构,科学家构建出人工神经网络ANN。我们类比人类的神经元,通过计算机模拟出神经元的功能:
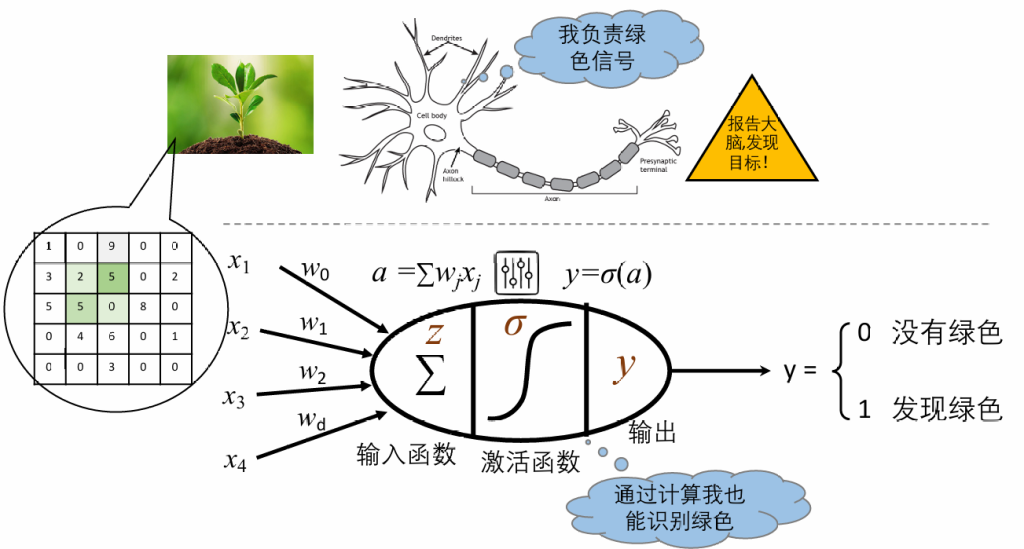
如果其中的激活函数σ ()是sign()符号函数的话,这个神经元就是之前学过的感知机。
我们可以通过感知机来模拟与或运算:
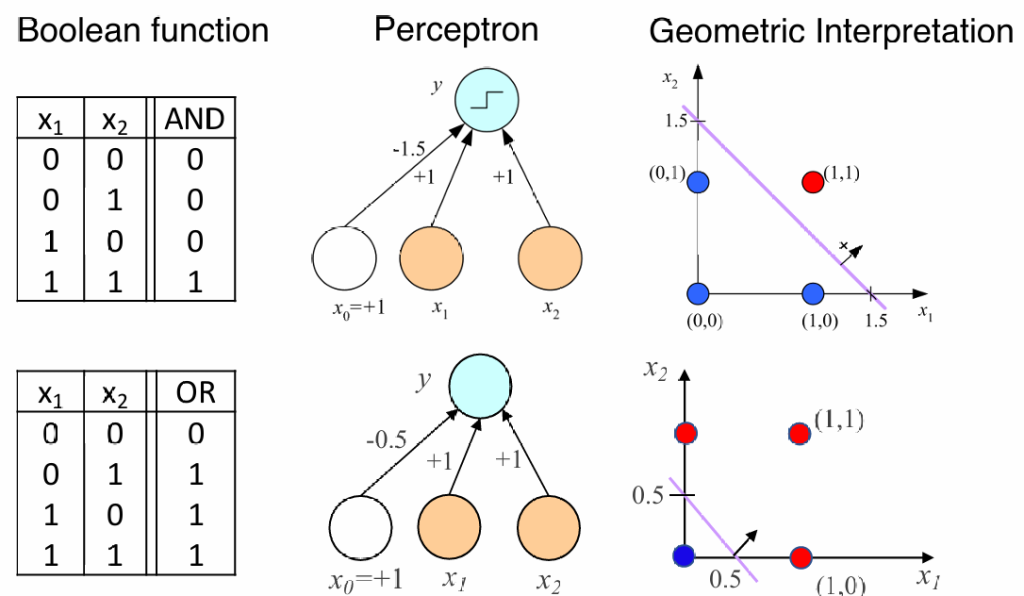
同时,当我们添加一个“隐藏层”,我们就能模拟一些非线性操作,比如异或
除了符号函数,我们还可以选择其他的非线性的激活函数
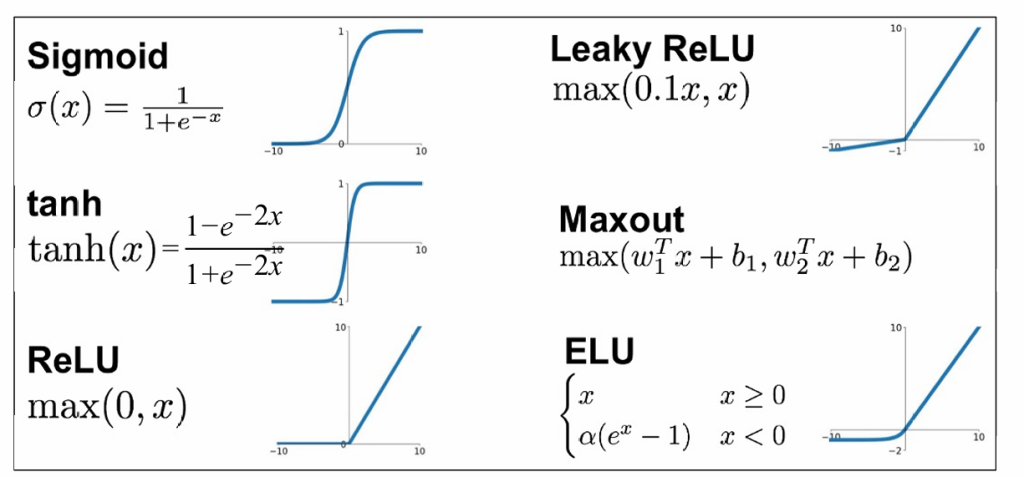
简单的多层感知机结构:
损失函数:
多层感知机在使用梯度下降法进行参数更新时采用的策略叫误差反向传播
假定我们现在有如下神经网络:
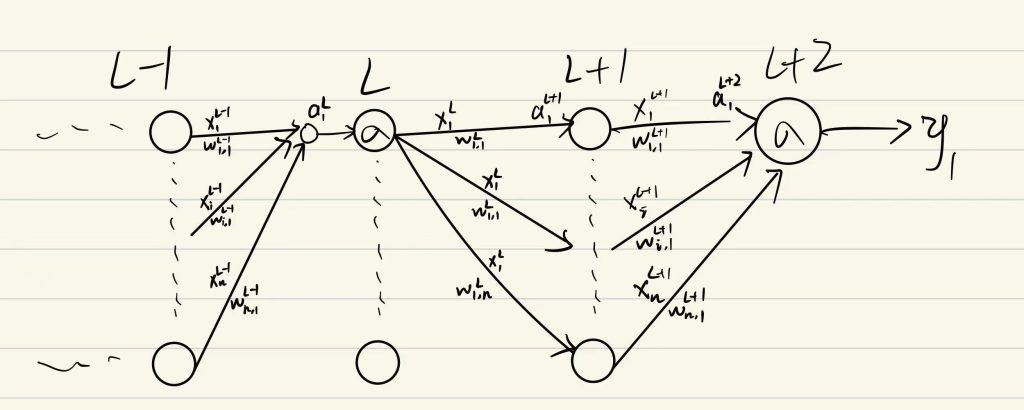
并对每个神经元(位于L层第j个)做如下抽象:
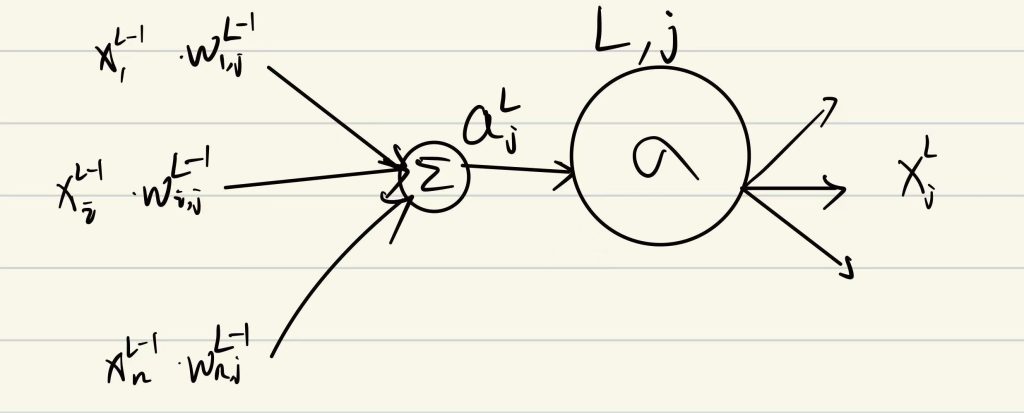
我们需要计算所有的
我们先关心输出层,我们需要计算所有的
容易得到
我们再考虑位于L层的第j个神经元
我们需要计算所有的
可以得到
现在,如果能计算出∂L/∂x,那么我们就能计算出我们想得到的所有数据。
我们考虑输出层神经元
我们需要计算:
注意到
注意,如果是中间层,则最后是求和的形式,因为x被使用n次
上面的推导非常复杂,但我们只需要知道:
我们将第一部分称为输入,后一部分称为误差;输入是wi,jL上对应的xiL,而误差δjL可以根据下面的式子递归计算

在递归计算梯度的时候会经常重复,可以使用动态规划优化
深度学习的特点:
- 自动学习数据表征
- 学习层次化表征
- 端到端学习
语言模型
Word to Vector
单纯使用ASCII码,机器无法理解数字的意义,无法理解单词与单词间的关系
one-hot编码:每个单词占有向量中的一位,这一位为1,其余为0;非常占用空间,并且不能反映词间关系
我们希望使用一种压缩的向量,并且能够反映词间关系
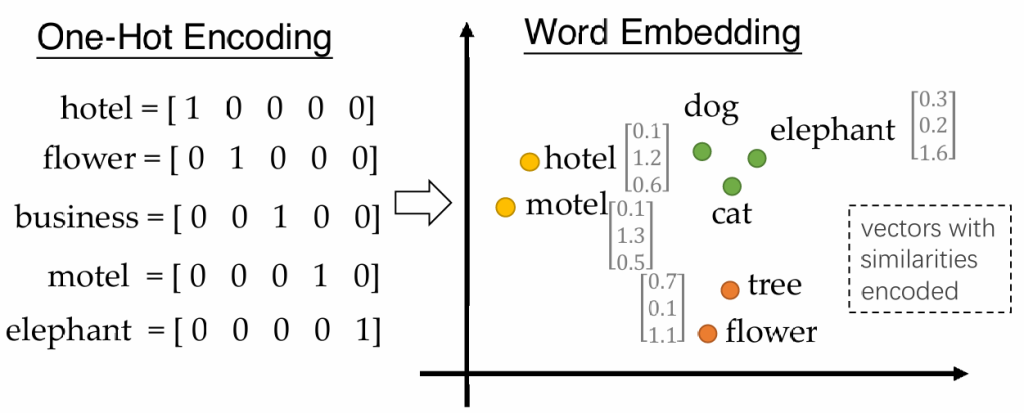
如何获得单词编码:
基本想法,如果未知单词和已知单词具有相似的上下文,那么认为这个未知单词和已知单词相似
算法:
- 准备一个大规模的文本库
- 给每个单词分配一个词向量
- 遍历文本,获取单词w及其两边的词c
- 根据向量相似度计算给定c后中间为w的概率
- 更新词向量,直至概率最大化
现在我们得到了词向量,我们应该怎么让计算机输出句子?
定义一句话x由w1,..,wn构成的概率为p(x)=p(w1,w2,…,wn),我们如何计算这个概率?
基于条件概率我们可以得出:p(w1,w2,…,wn)=p(w1)p(w2|w1)…p(wn|w1,w2…),而单词一般只和相近的单词有关,因此我们可以化简成只考虑前k个单词
那么我们如何获得这个条件概率?
——naive的想法是计数,但是一些细微的变化就会导致计数不准,所以我们可以使用词向量代替单词。词向量可以反映相似度,但是这种方式还不能反映词与词间的顺序,所以我们将多个词向量进行拼接。这种方式的问题是输入的长度不可变,并且标点符号等会对其产生很大影响。
我们的要求:
- 处理变长序列
- 跟踪长期依赖关系
- 保存有关顺序的信息信息
- 在语句间共享参数
循环神经网络RNN
每次输出一个单词,在输出下个单词时,将这个单词也输入到模型中
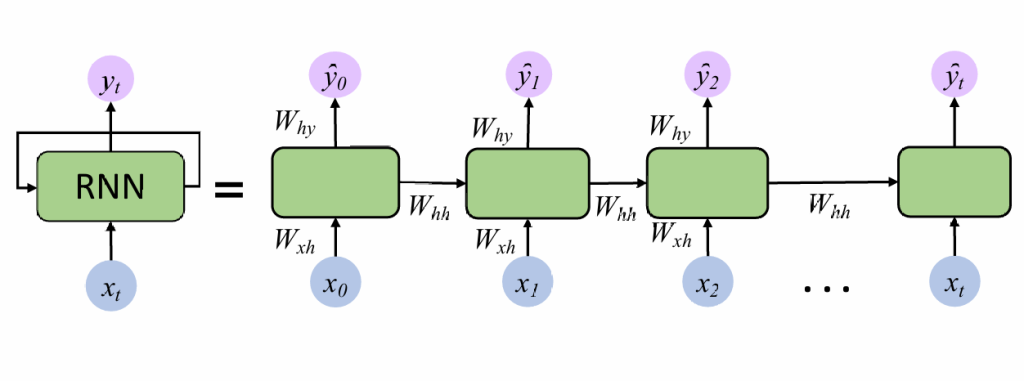
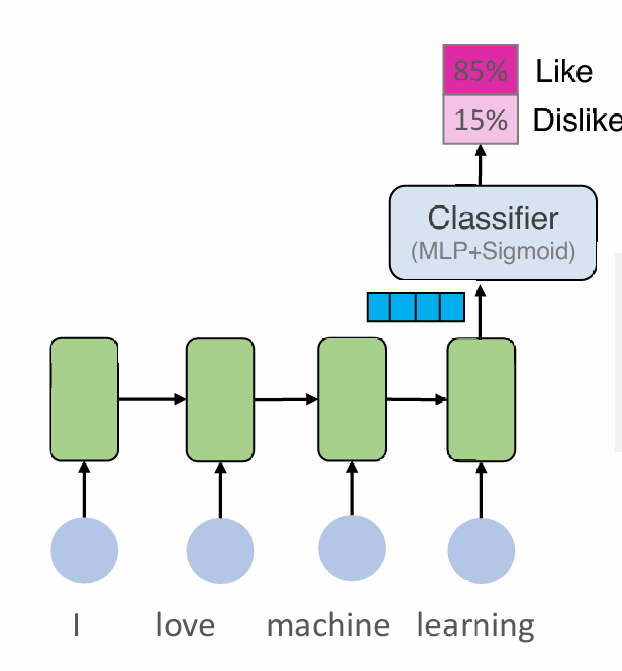
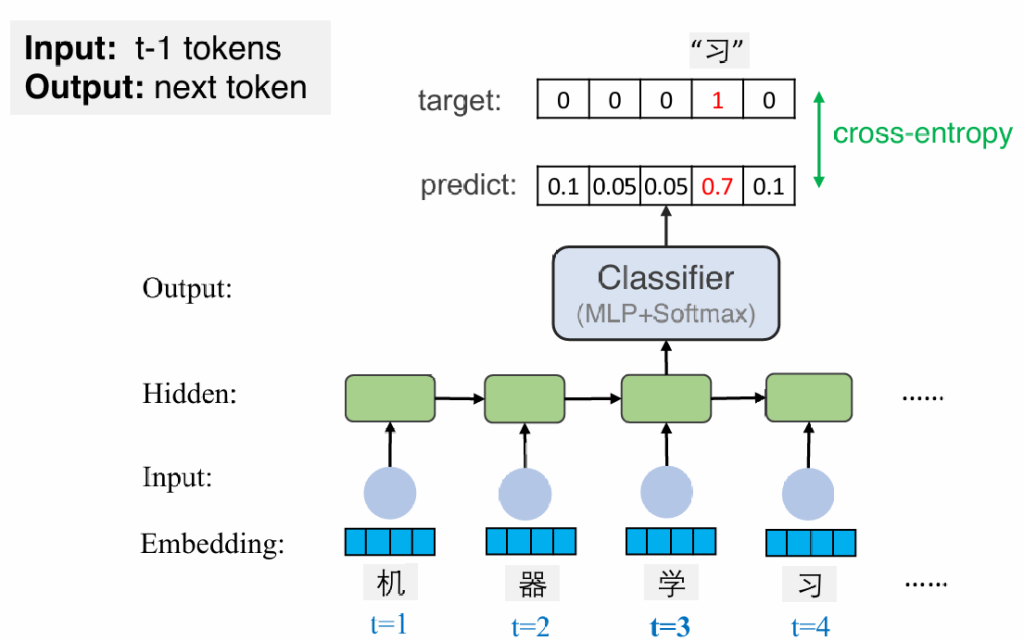
循环神经网络的应用:
语句分类:
文本生成:
Transformer
RNN的编解码器
使用两个RNN,一个作为编码器,处理输入序列,一个作为解码器,生成输出序列。通过这个通用的模型,我们可以完成语音转文字、翻译等工作
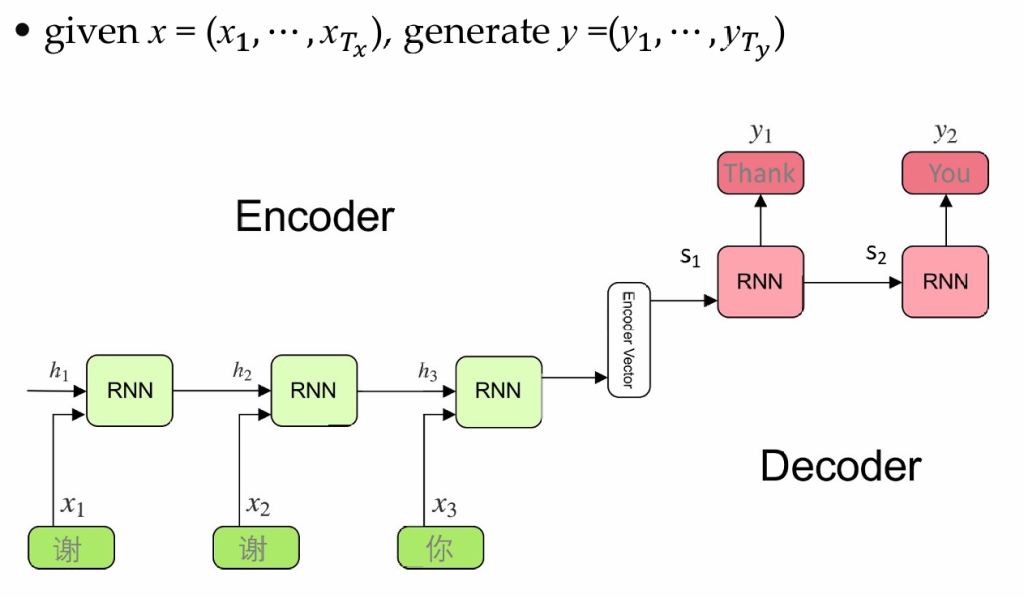
编码器的任务是将输入的序列压缩成一个向量c,解码器的任务是基于向量c生成序列,并通过分类器将生成的序列转换成自然语言
训练过程:通过生成的y和真实值做比对,最小化交叉熵损失函数
除了文本生成、翻译等功能,还可以用于图像生成等。
但是RNN的缺点是无法理解长文本,因为向量c的表达能力是有限的,会带来很大的信息损失。改进:动态编码器
动态编码器会生成多个ci,解码器需要根据当前生成的序列,自行选择关联度更高的ci,这也被称为注意力机制
注意力机制
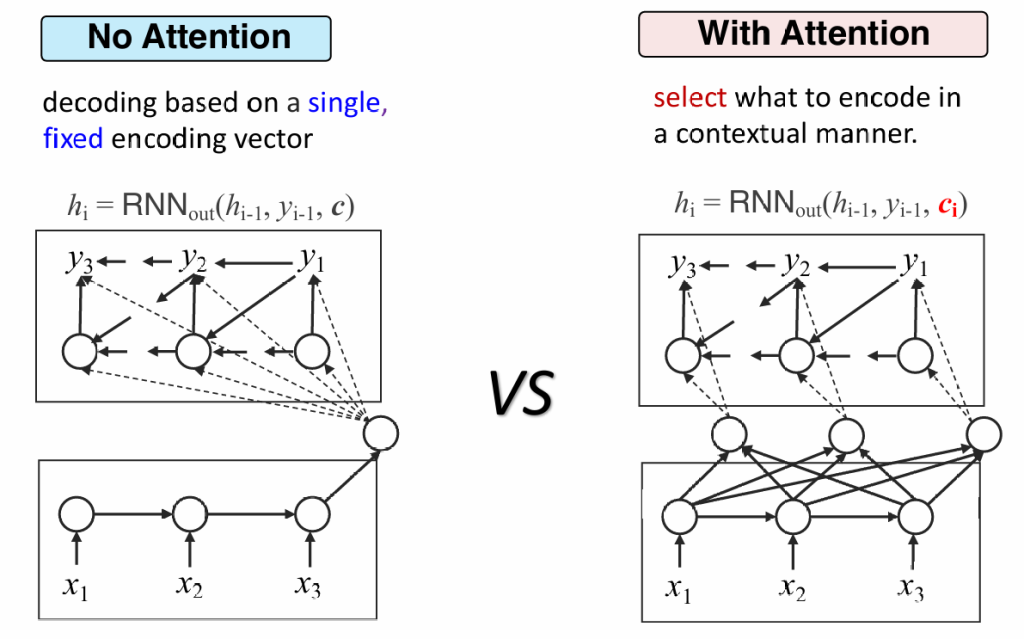
那么我们如何选择最合理的c?
——训练一个神经网络,输入为解码器的状态及所有c,输出所有c的分数,选择分数最高的
Transformer
我们将注意力机制进行拓展,我们希望在编码过程中也使用注意力机制,克服掉RNN不能并行的缺点。
我们把注意力机制抽象成如下过程:
根据当前状态,选择关联度最高的词语,这个过程定义为Query/检索;检索的依据称为Key;通过检索得到的值称为Value
假设我们现在想要获取一个句子中“it”语义,则我们进行检索,根据每个单词的key打分,得到的分数为value
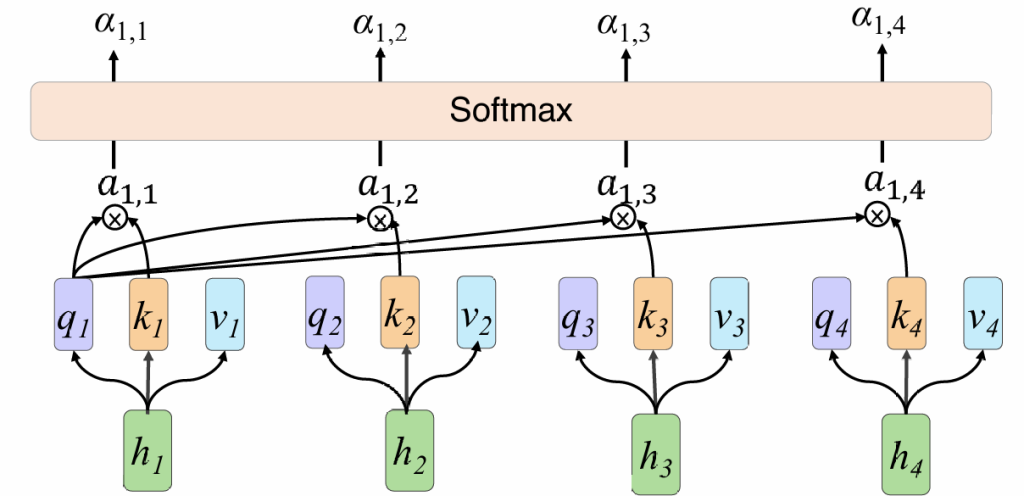
具体步骤:
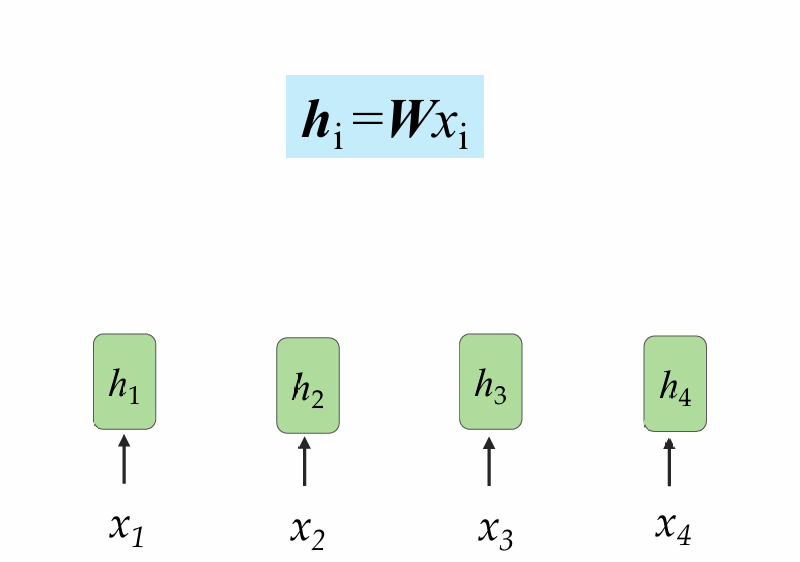
设输入为x={x1,x2,…,xn}
1.编码
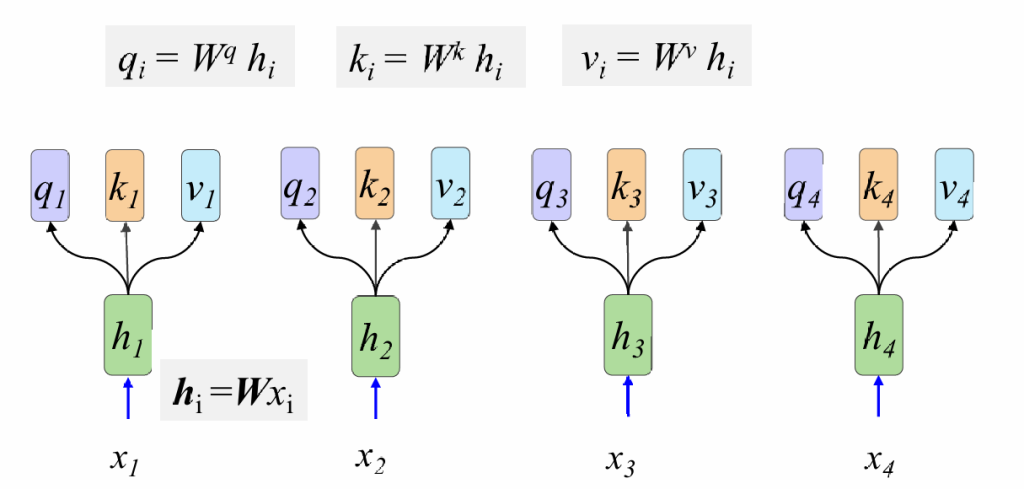
2.计算Q,K,V
3.计算分数并归一化
我们以h1做query为例,h1用自己的q1分别与k1-ki计算分数a,然后通过softmax归一化得到α
其中d为q和k的维度
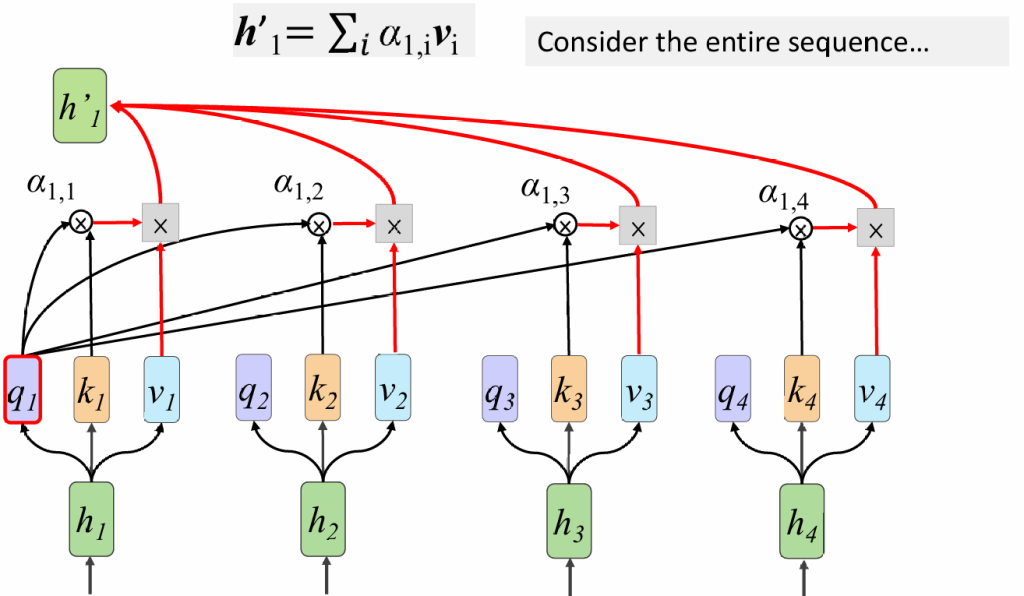
4.融合注意力与value
我们把得到的分数,和value结合,得到h1‘-hi’
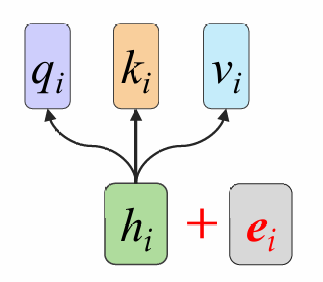
我们对上面几步抽象成矩阵计算:
第一步:H=WX
第二步:Q=WqH;K=WkH;V=WvH
第三步:A=KTQ/\sqrt{d}; A’=softmax(A)注意这里一定要除\sqrt{d},ppt是错的
假设原来是[10,20,30],除\sqrt{d}后是[1,2,3],前者softmax结果是[2.06106005e-09 4.53978686e-05 9.99954600e-01],后者是[0.09003057 0.24472847 0.66524096]
第四步:H’=VA’
这些矩阵运算可以用gpu加速,但是上面的过程丢失了词语间的顺序,我们需要补充一个位置编码,将顺序作为模型输入(onehot编码,在哪一位哪一位就是1)
完整的transformer:
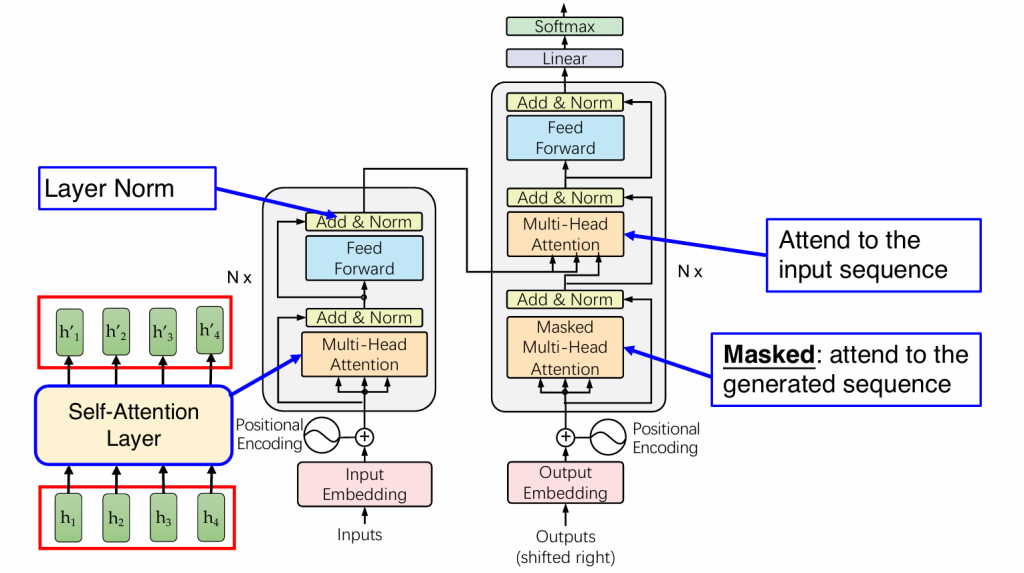
(decoder在复习ppt里没有,懒得写了)
大语言模型LLM
预训练语言模型
在一些情况下,我们的数据量不足以训练一个transformer,我们选择先让模型理解自然语言,然后再在小数据上微调。
我们介绍一种使用最广泛的预训练模型BERT
BERT的训练目标是理解自然语言,以此为基础的训练任务有两个:1.输入随机遮罩的句子,预测被遮罩的词语;2.给定两个句子,判断两句是否是上下文关系
微调应用:句子分类;词语标记;语句间关系预测;阅读理解Q&A;
大语言模型LLM
(在复习ppt里没有,主要介绍了大模型微调;参数化微调(只更新一部分参数);提示词工程;RAG检索增加生成(用户对数据进行筛选排序,然后和问题一起发给大模型);)
卷积神经网络CNN
机器如何识别图片?
如果直接把图片作为矩阵输入,细微的差别就会导致模型输出不同;
将图片的特征提取,将特征喂给模型,但是特征提取需要人工标注;
——基于深度学习的自动特征提取
标准神经网络的问题:
- 丢失图片的位置信息(整个图片是一个向量)
- 关注整张图片,不会将注意力集中
- 对于信息的位置敏感
- 参数量过大
从MLP到CNN:
首先简化全连接层,让网络关心局部特征
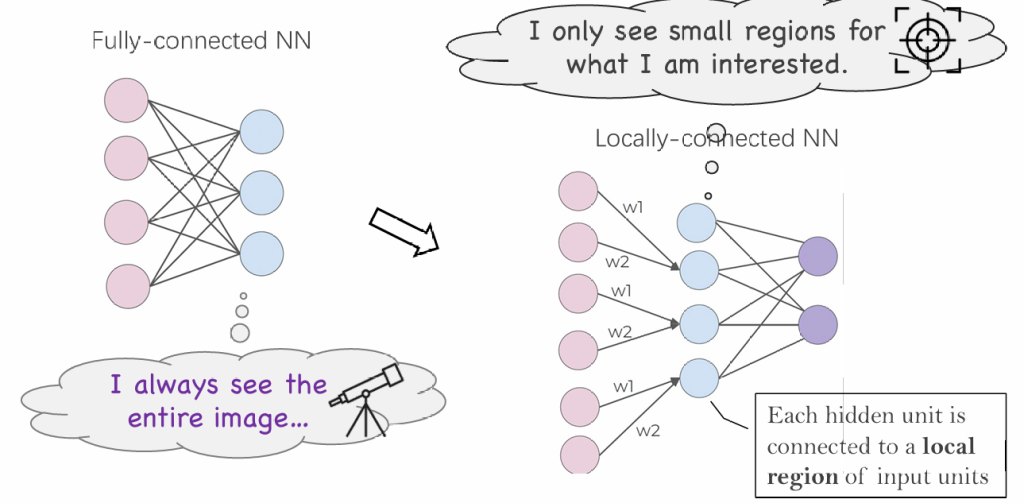
这个过程实际可以用卷积完成,将几个点的数据通过卷积合并成一个数据
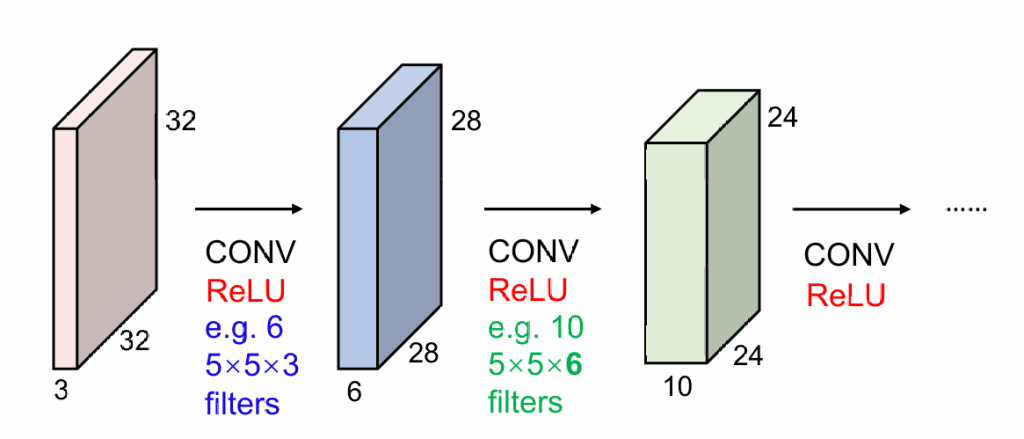
实际情况下,因为图片有RGB三通道,所以实际我们做的是3维卷积。比如3*5*5的卷积核就会将75个值合并成1个
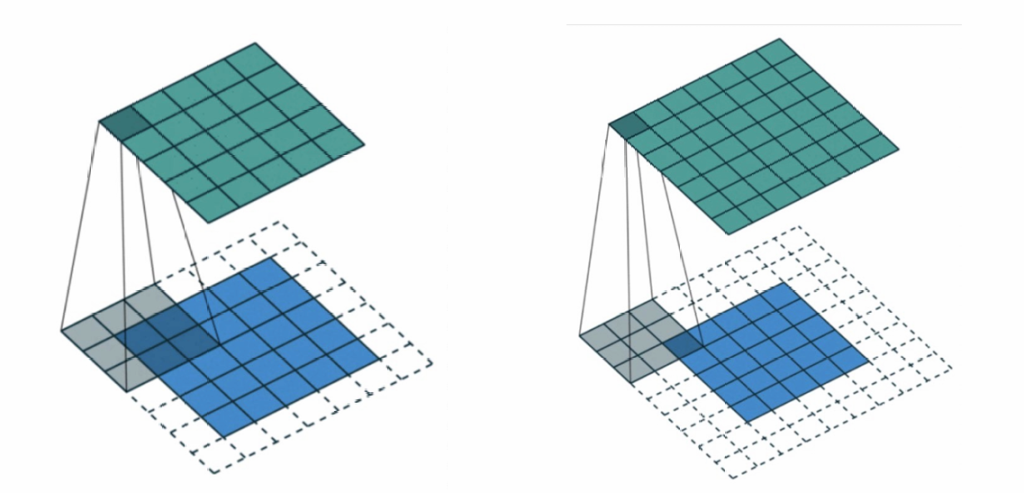
针对图片缩小的问题,我们采取填充(padding)的方式解决;
同时,如果我们想缩小卷积后的大小,我们采用池化(pooling),即卷积核跳过一些位置
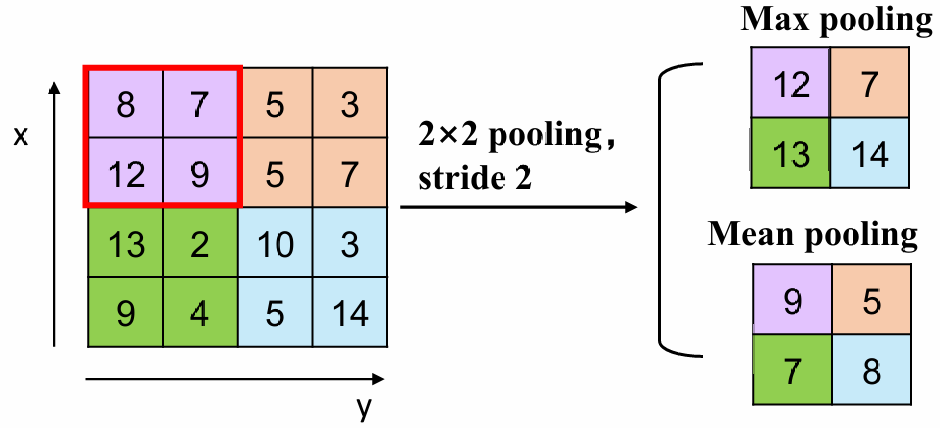
假设我们使用N*N的原图片,F*F的卷积核,填充宽度为P(如果宽度为1则边长为N+2),池化为S(stride),则输出大小为(N+2P-F)/S
思考:
我们可以把用CNN处理文本(代替MLP)吗?——可以,用卷积核卷连续几个词向量
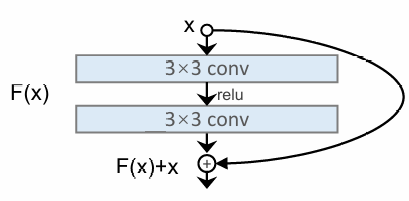
我们在实践中发现在卷积层叠加到很高后,效果反而不如较少的层次,原因是后续的卷积层丢失了原有的信息,为此我们使用残差网络,将原始数据和卷积后的数据都传播到后面
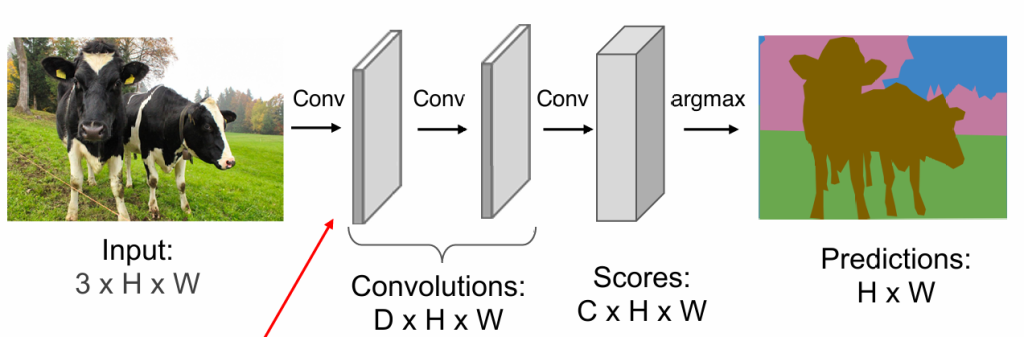
机器视觉CV
机器视觉的任务:图片分类、图片分割、物体识别、图升文、文生图
图片分割

显然我们不能让模型对单独的一个像素进行分类,因为几千万像素不能逐一进行分类
——我们能否通过卷积神经网络,得到特征,然后得出分类
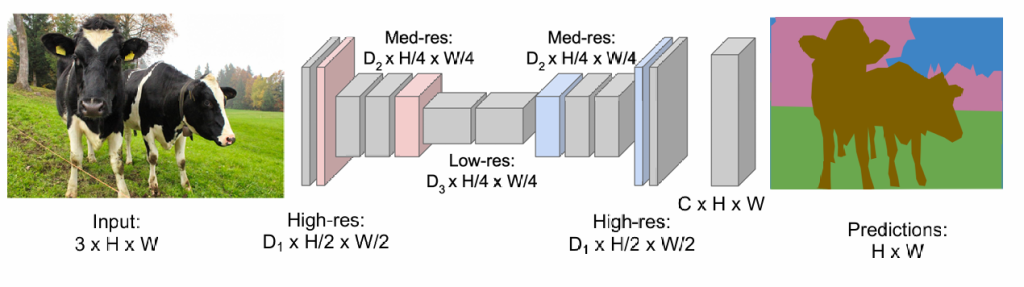
我们似乎没有必要对整个图片进行划分,我们可以先在小图片上划出轮廓,再复原大图片
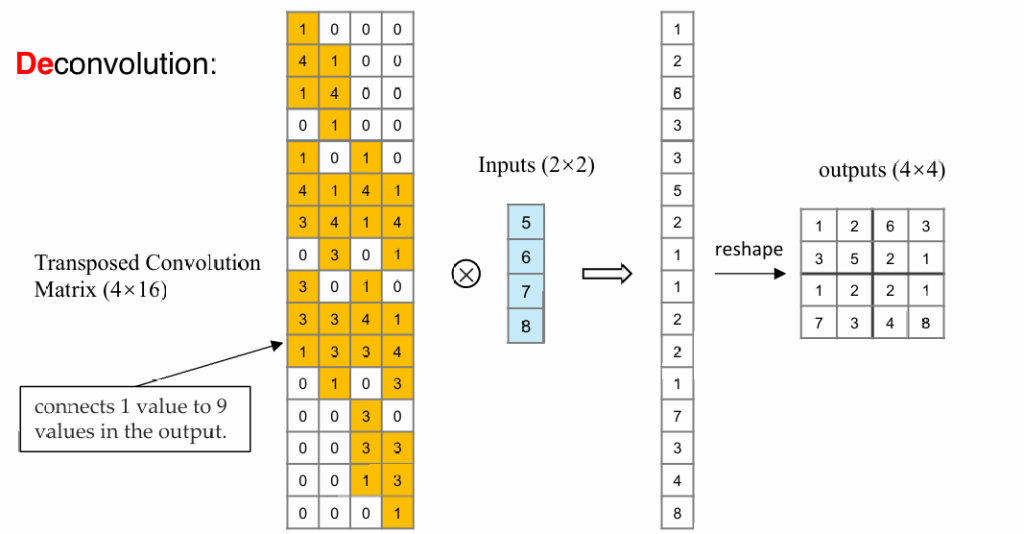
现在我们考虑如何复原图片(unpooling):
从正向的卷积来看,我们可以通过将图片及卷积核铺开,将卷积操作变成矩阵Cm×n与向量i的乘法
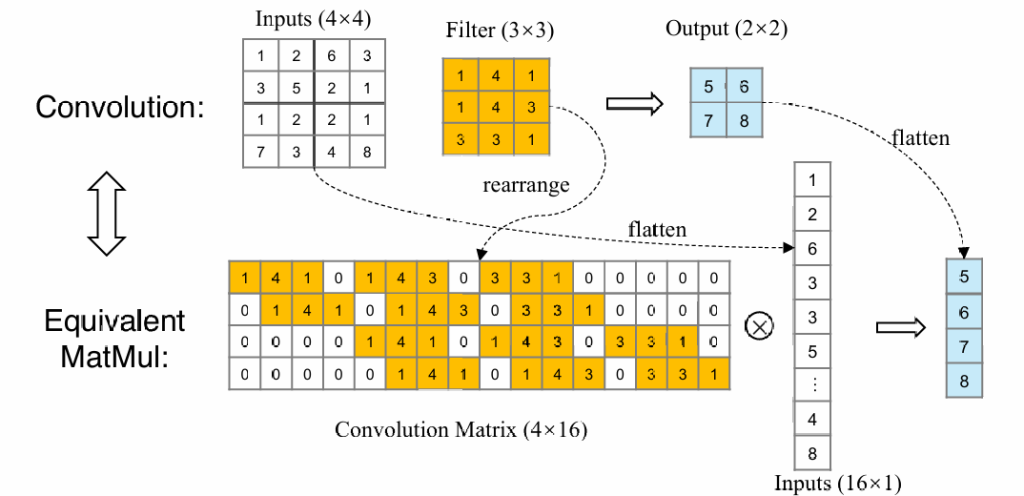
所以我们可以通过反向乘一个n×m的矩阵,将卷积后的结果复原成原始图片的大小(注意不能完全复原成原始图片,需要学习矩阵参数)
物体识别
识别=分类+定位

分类很好解决,只需要训练一个分类器;主要问题是如何划分图片?
我们使用“selective search”——一个传统的机器视觉算法,能够给出可能出现目标的范围

当我们获得这些分块的小图片,我们对这些图片进行卷积可以完成目标(slow r-cnn),但我们仍觉得分块过于多,所以我们先对整张图进行一次卷积,再根据小分块裁剪卷积结果,提升运行速度(fast r-cnn)
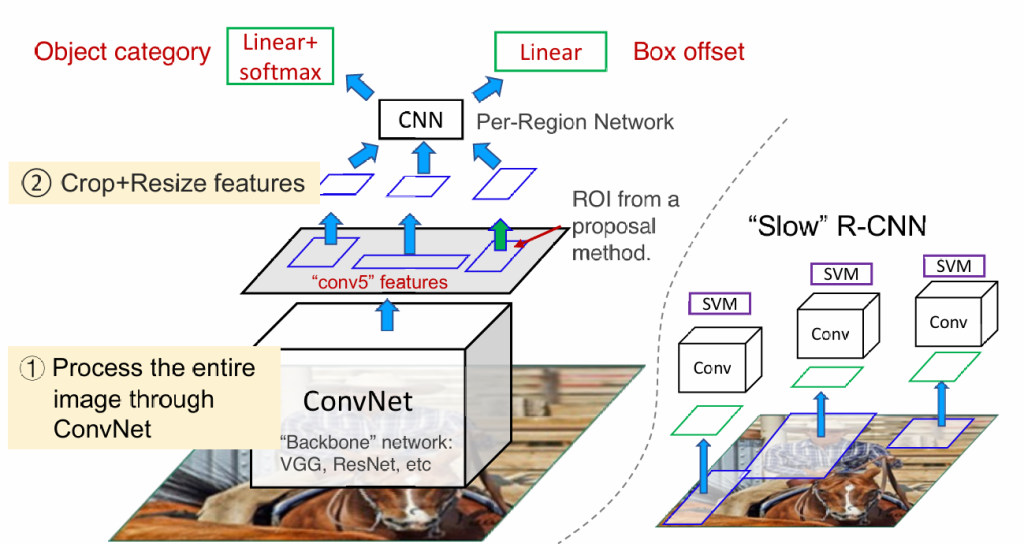
除此之外,我们还可以通过训练神经网络进行图片划分(faster r-cnn),还有一些其他算法可以提升速度(YOLO)
图生文
类似于翻译问题,我们仍拆分成编解码器,参照transformer,将图片通过卷积神经网络提取特征,然后接入自注意力机制;甚至可以直接将分块的原始图片输入给transformer,不使用卷积神经网络(Vision Transformer-ViT)
视觉语言模型VLM
在ViT中我们发现transformer不仅能理解文字,还能理解图片,那么我们可以训练一个支持多种类型输入输出的transformer
clip:对文字和与之对应的图片采用两个encoder进行编码,最大化两组编码的相似度
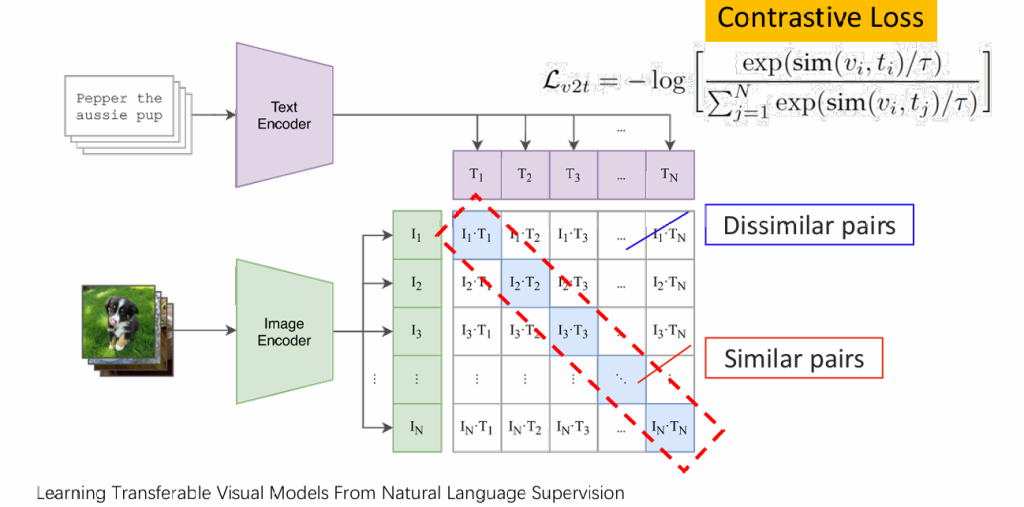
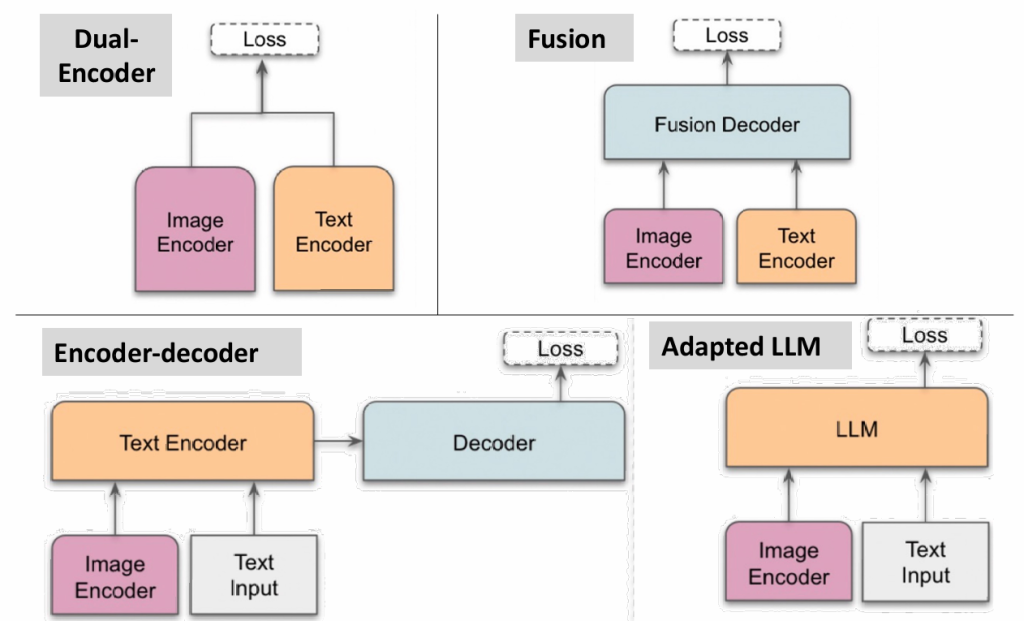
CLIP对应下图中的左上角,还有些不同的架构
聚类
我们希望在没有标签的情况下,让模型自行将数据分类。在大规模数据中,我们无法使用k-近邻算法,因为存储难度太大,我们选择记录只每个簇的圆心。
k-means把簇的圆心定义为簇内点的均值,需要人为给定k
k-均值算法由以下四步来完成:
- 随机的选择k个对象作为目前划分的簇的初始簇中心
- 对剩下的每个对象,计算与各簇中心的欧氏距离,将它分配到最相似的簇
- 使用上次迭代分配到该簇的对象,计算新的均值
- 使用新的均值作为新的簇中心,重新分配所有对象,直到分配稳定
复杂度:O(Iknd);其中n 是对象的数目, k 是簇的数目, I 是迭代的次数, d是向量的维数
受初始中心的影响,可能导致迭代次数增加或陷入局部最优
优点:
- 有可解释性
- 效率高
缺点:
- 每个簇都是球形
- 在一些抽象数据中,“均值”难以定义
- k需要人工指定,不一定合适
- 对异常值敏感
降维
降维方法:PCA主成分分析(线性)Autoencoder自编码器(非线性)
PCA主成分分析
以以下数据为例
A = [2.5, 2.4]
B = [0.4, 0.7]
C = [2.2, 2.9]
1.计算样本均值X及协方差矩阵S
定义协方差及协方差矩阵(以2维为例,若三维则为xyz),(n为样本数量)
在例子中:

2.解出协方差矩阵S的特征值λ,即|S-λI|=0的解
解二元一次方程得
进而得到与λ对应的特征向量(即Sv=λv)
特征向量满足如下式子:
需要设v=[x,y]然后解出x,y的比例,再归一化到单位长度
对于λ1:
解得
以上两个约等于是因为计算误差导致的,实际上会是一个值。
再进行归一化,v1=[0.713,-0.696]
对于λ2同理,v2=[0.696,0.713](因为是2维所以可以直接看出来,三维不行)
两个主成分的表示:
主成分的贡献度p:(经证明主成分的方差就是特征值大小)
对示例情况:
F1贡献度=0.06/(0.06+2.53)=0.02
F2贡献度=2.53/(0.06+2.53)=0.98
可以根据贡献度从大到小,对所有主成分进行排序,然后根据累计贡献度要求选出前几个主成分
PCA的应用:人脸识别
通过人脸数据库,获得“平均脸”,然后选择重要的主成分;对输入图片计算主成分,与平均脸比对就能判断其是否为人脸
Autoencoder自编码器
自编码器是一个神经网络,其输出目标是还原输入
PCA算法可以抽象成一对编解码器

实际的自编码器,编解码器是需要训练的神经网络

我们可以使用自编码器完成图片复原、相似图片搜索等功能,以及用于CNN
生成式模型
GAN
回忆:语言模型也是生成式模型,我们学习的是下一个词语的概率
仿照语言模型,我们在生成其他数据如图片时,学习的也是概率
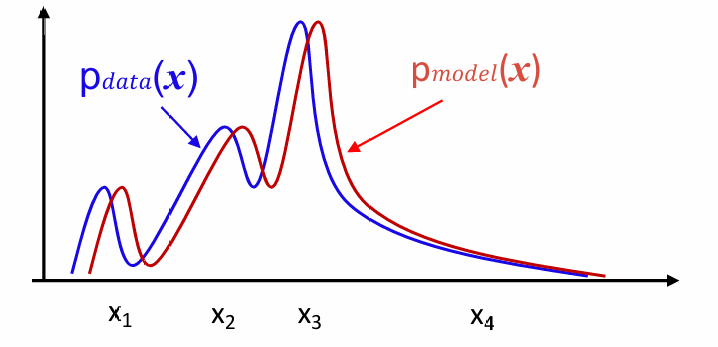
问题:
我们如何表示图片的概率
我们如何使pmodel接近pdata
表示图片的概率:
我们通过随机数让生成器G产生图片,就如同掷色子,通过大量的生成的图片的分布反映概率分布
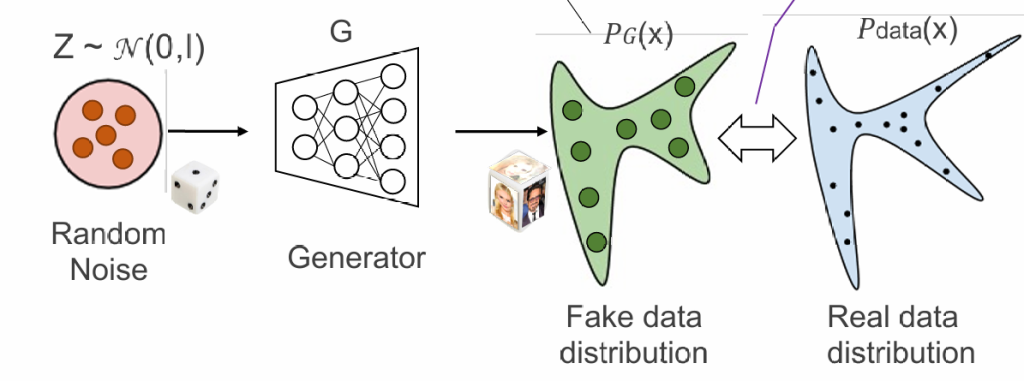
使pmodel接近pdata:
即希望模型只生成真图片,不生成假图片,生成的假图片越少,说明二者的概率分布越接近
引入一个判别器:判断一张图片是否由ai生成,当生成模型可以以假乱真,那么说明分布是一致的。
在这种情况下,生成器和判别器的目标是相反的,二者构成了“生成对抗网络”GAN
判别器的训练:(损失函数使用交叉熵定义)

生成器的训练:(损失函数与判别器相反)
因为生成器看不到真实图片,所以少了一项

需要注意的是,训练开始时,需要有一个已经预训练过的判别器,否则训练结果不好。
深度卷积生成对抗网络DCGAN
使用逆向卷积作为生成器,使用卷积神经网络作为判别器

针对DCGAN,研究人员发现了一些有趣的现象。
加上我们训练好了一个生成器,然后我们已知某些随机种子对应着生成某类图片;当我们给这些种子进行线性组合,生成的图片仍是这个类型;甚至,类间的随机种子加减后的结果能反映出图片类型的增删

Conditional GAN
能够按照需求生成图片
我们把条件分别输入生成器和判别器,然后进行训练,也可以看作一种翻译器

CycleGAN
Conditional GAN是监督学习,需要大量的成对数据,而cycleGAN的目标是无监督学习。在没有成对示例的情况下将图像从源域 A 传输到目标域 B。

GAN本质上是一个从随机分布到图片概率分布的概率转换器;而CycleGAN需要的是从图片概率分布到图片概率分布的概率转换器

模型结构:

通过反向生成器GBA尝试复原图片,最大化复原图与原图的相似度;GAB训练目标不变。如果GBA能复原图片,说明生成的假图片一定包含了原图的信息
变分自编码器Variational Autoencoder-VAE
GAN生成图片需要随机变量z,但是我们找不到z的规律,无法通过定向需求产生图片
我们想到使用Autoencoder,使z是一张原始图片的压缩表示,这样的z是有意义的,可以用来定向生成图片,但是Autoencoder中z是离散分布的,我们要想办法让z的分布式连续的,比如符合高斯分布
VAE:强制编码器输出均值和标准差(可以确定为一个高斯分布),解码器的输入是符合这个高斯分布的一个随机值;这样训练出的模型会将特征隐藏在高斯分布中,而满足这种高斯分布的随机种子生成的图片具有相同的特征,但又各不相同。

GAN和VAE的局限性:降维后的z的表达能力有限,和原始图片差别非常大;所有内容都是一次生成的
去噪扩散模型
希望模仿人类的绘画过程,一步步生成图片
模型结构:原始图片是随机噪声,经过多层生成器得到图片

训练过程:在一张图片上随机添加噪声点,再训练模型将其复原(对每一层分别训练,而不是一起训练)

强化学习RL
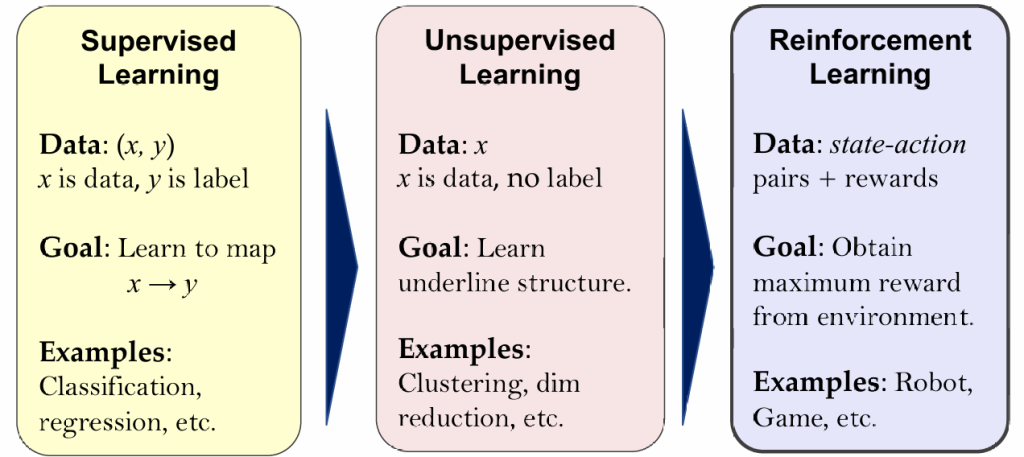
监督学习、无监督学习、强化学习对比:
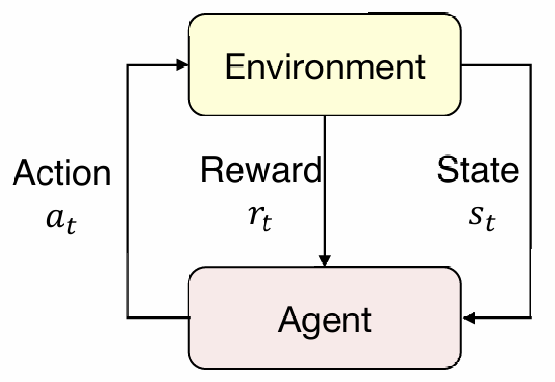
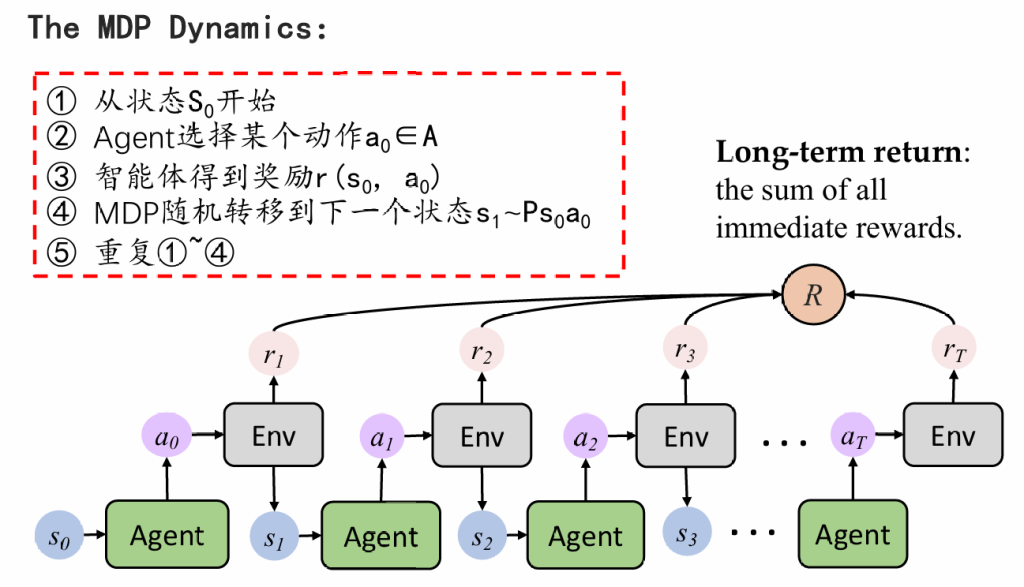
强化学习的基本结构:
agent生成一个action,环境返回state和reward;agent再根据state生成新的action
我们首先定义一个马尔可夫决策过程:
我们将训练抽象成如下图的多次决策,每次决策会带来状态转移,并获得一定的奖励/惩罚;而我们的目标是找到奖励最大的一条路径
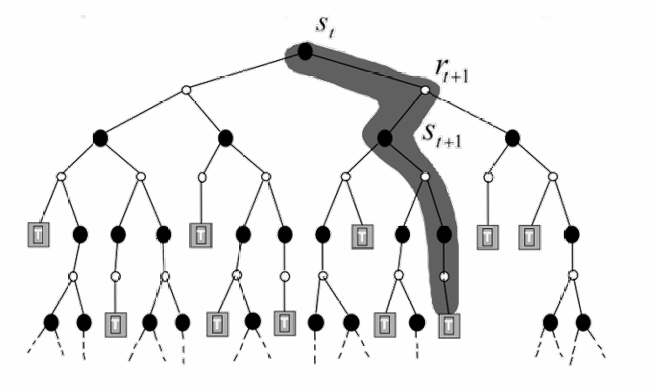
RL的学习过程:
Q-Learning
定义:Q函数:输入为当前状态和行为,输出为未来可获得奖励的期望
如何得到Q值:
1.蒙特卡洛:通过遍历后续所有情况/随机计算几种后续情况,计算平均的奖励值;但是会耗费大量时间
2.递归估计:根据递推关系Qt=rt+γmaxa{Qt+1},采用动态规划的方式,填写一个Q值表,直至表填满(递归关系不唯一)
Q函数的问题:只能适用于走格子这种简单的游戏,我们无法将Q值表真正填满,因此我们使用神经网络来拟合Q函数
DQN

损失函数:

在训练过程中,我们存储状态转移的四元组D = {(s(1),a(1), r(1), s’(1)), …, (s(N) , a(N), r(N), s’(N))},DQN在对整个D进行优化时的损失函数:

问题:Q也是根据模型变化的,目标值不稳定,于是我们另外指定一个网络(target Net),专门用于生成Q,整个网络的参数是固定的,每隔一段时间将Q Net的参数复制过去。

策略学习
前面我们都在学习Q值,现在我们想直接根据环境S得出行动a,或者说给出某个行动ai最优的概率
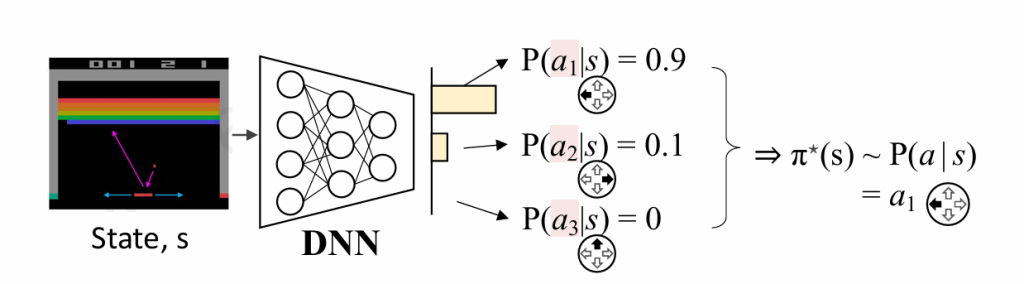
转换成了一个分类问题,我们使用未来能获得最大评价奖励的a作为目标值。
我们还是通过多次实验的方式得到平均的reward
经过数学推导我们可以得到损失函数:
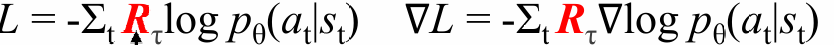
参数更新及梯度表示:

基于RL的文本生成
我们之前学到的文本生成,都在预测下一个词语的概率,这可能导致语法正确性、连贯度等受影响;如果我们根据这些指标给词语打分,可以一定情况下优化模型的输出。
Just found win456. I often play on my phone. How good is their mobile site? win456
Heard some buzz about American Matka connected to this site too. Seems a bit dodgy to me, but hey, do your homework before jumping in! american matka
Vina24h, hum? I’m intrigued. Let’s dive in and see what they offer. Fingers crossed! Explore it here: vina24h
Heard good things about the Live789 Club. Hoping to check it out soon and see if the hype is real. Anyone got tips or know if they offer a good loyalty program Would appreciate the insider scoop before I dive in A live789 club
Looking for a specific game so I went to Selcuksportshdxyz.com using ‘selçukspor hd’ as a search term. It’s a bit hit or miss but it might work for ya. See if they got what you want: selçukspor hd
Just wanted to give a shoutout to Selçuk Sportshd. I’ve been using their site for ages to watch my favorite sports. The quality is generally good, and it’s pretty reliable. My go-to spot! : selçuk sportshd