序言
斐波那契数列
algo1:
FIBO1(n)
if n=0 then return 0;
if n=1 then return 1;
return FIBO1(n-1)+FIBO1(n-2);指数级(exponential to n)
algo2:
FIBO2(n)
if n=0 then return 0;
create an array f[0...n];
f[0]=0;f[1]=1;
for i=2 to n do
| f[i]=f[i-1]+f[i-2];
end
return f[n];
多项式时间(polynomial), n2
algo3:
斐波那契数列有通项公式
大O表示法 Big-O Notation
上界: f(n) is O(g(n)) (or f(n)=O(g(n)) ), 当且仅当 存在常数c>0, 常数n0≥0; 使得对于所有n≥n0, 0≤f(n)≤c·g(n).
下界: f(n) is Ω(g(n)) (or f(n)=Ω(g(n)) ), 当且仅当 存在常数c>0, 常数n0≥0; 使得对于所有n≥n0, 0≤c·g(n)≤f(n).
f(n) is Θ(g(n)) (or f(n)=Θ(g(n)) ), 当且仅当 存在常数c1>0, c2>0, 常数n0≥0; 使得对于所有n≥n0, 0≤c1·g(n)≤f(n)≤c2·g(n).
n! is 2Θ(n log n)
斯特林公式:
数字的算法
基本算数
除非使用1进制,否则计算机进制不影响复杂度
加法复杂度是O(n),因为读取至少是O(n),无法优化
乘法算法
按竖式计算的方法:复杂度是O(n2),但*2操作是O(1),所以可以优化
Al Khwarizmi
- 两个乘数分开写
- 左边/2,右边*2
- 直到左边变为1
- 去掉左边为偶数的行
- 将右边的数相加

公式:
algo:
MULTIPLY(x,y)
if y=0 then return 0;
z=MULTIPLY(x,[y/2]);
if y%2=0 then
| return 2z;
| else return x+2z;
end复杂度分析:递归n次,每次都可能有加法,加法是O(n),所以还是O(n2),还有优化空间
除法算法
DIVIDE(x,y)
if x=0 then return (0,0);
(q,r)=DIVIDE([x/2],y);
q=2·q, r=2·r;
if x is odd then r=r+1;
if r≥y then r=r-y;q=q+1;
return (q,r)复杂度分析:递归n次,每次都可能有加法,加法是O(n),所以是O(n2)
模运算
x≡y mod N ⇔ N divides (x-y)(N被(x-y)整除)
≡:语法/语义上等于
运算法则:
- 替换:x≡x’ mod N and y≡y’ mod N, ⇒ x+y≡x’+y’ mod N and xy≡x’y’ mod N
- 满足加法/乘法 交换/结合律、乘法分配律;
- 模运算可以随时应用在任何阶段:2345≡(25)69≡3269≡169≡1 mod 31
模加、模乘、模指数
模加:input (x,y) output (x+y) mod N,时间复杂度O(n)(加法+减法),n为长度
模乘:input (x,y) output (xy) mod N,时间复杂度O(n2)(乘法+除法),n为长度
模指数:input (x,y) output (xy) mod N,模指数过于大,如何计算:
first idea:x mod N->x2 mod N->x3 mod N->…->xy mod N,仍然很大
second idea:x mod N->x2 mod N->x4 mod N->…->x2^[log y] mod N,对于一般的y,忽略y二进制表示为0的位,例:
x25 mod N=(x16 mod N)(x8 mod N)(x1 mod N)
algo:
MODEXP(x,y,N)
if y=0 then return 1;
z=MODEXP(x,[y/2],N);
if y%2=0 then
| return z2 mod N;
| else return x·z2 mod N;
end复杂度分析:递归n次,每次都做n位数的乘法,O(n3)
欧几里得的最大公因数(gcd)算法
algo:
gcd(x,y)
Two integers with x≥y
if y=0 then return x;
return gcd(y,x mod y);Lemma: If a≥b≥0, then a mod b < a/2;
Proof: 按b关于a/2的大小关系分类讨论即可
复杂度分析:最多循环n轮,每次做除法,O(n3)
Lemma: if d整除x和y, and 存在整数a,b使得d=ax+by, then d=gcd(x,y)
例:10,15最大公因数为5,a,b取值-1,1
Proof:
- 显然d≤gcd(x,y);
- gcd(x,y)被x、y整除,也被d=ax+by整除,所以d≥gcd(x,y);
- 所以d=gcd(x,y)
扩展欧几里得算法:用于求出d的同时得出整数a、b
algo:
extended-euclid(a,b)
Two integers with a≥b
if b=0 then return (1,0,a);
(x',y',d)=extended-euclid(b,a mod b);
return (y',x'-[a/b]y',d);//每次进行a mod b实际减少了[a/b]个y
end乘法逆元和模除
乘法逆元:x是a mod N的乘法逆元,if ax≡1 mod N
乘法逆元至多有一个,可以写作a-1,乘法逆元可能不存在
Lemma: 不存在乘法逆元当且仅当gcd(a,N)>1(or a与N不互质)
Proof:
- gcd(a,N)>1⇒不存在乘法逆元
- gcd(a,N)整除ax+kN,ax+kN≡ax mod N ⇒ ax mod N>=gcd(a,N)>1
- gcd(a,N)=1⇒存在乘法逆元
- ax mod N = ax+kN, then gcd(a,N)整除ax+kN=ax mod N
- gcd(a,N)=1, 应用拓展欧几里得算法,给出x,y使得ax+Ny=1,then ax≡1 mod N,x是a的逆元
模除(注意不是取余数,也不是(a/b) mod N)input(a,b) output c that (b*c) mod N=a mod N
在模除中,被a除相当于乘a的乘法逆元,所以如果乘法逆元存在,可以用拓展欧几里得算法在O(n3)时间内求得。
例:
- 求(11/4) mod 5,4的乘法逆元是4,所以即求(11*4) mod 5=4
- 求(45/7)mod 10,7的乘法逆元是3,所以即求(45*3) mod10=5
素数
素数测试
费马小定理:p为质数,则任意1≤a<p,ap-1≡1 mod p
Proof:
- 取集合S={1,2,3,…,P-1}={a mod p, 2a mod p, 3a mod p, …, (p-1)a mod p}(注意两个集合数值一一对应但是顺序不对应)
- 证明两个集合一一对应:若不一一对应,则必有ai≡aj(mod p),导致了i≡j(mod p)⇒i=j矛盾
- 将对应位置的元素相乘,(p-1)! ≡ ap-1·(p-1)! (mod p)
- 两边同除(p-1)!(与p互素所以可以除)
- 所以ap-1≡1 mod p
对应的素数算法:
primary(N)
pick a < N at random;
if aN-1≡1(mod N)then
| return yes;
| else return no;
end但是,合数可能通过费马测试。Carmichael数如561=3·11·17,对于任意a<561,有a560≡1;
除了Carmichael数外,我们有 对于任意合数,如果存在一个a不满足aN-1≡1 mod N,那么a<N至少有一半不满足aN-1≡1 mod N。
Proof:
- 存在1个aN-1!≡1 mod N
- 假设1个bN-1≡1 mod N
- 那么(a·b)N-1≡aN-1·bN-1≡aN-1!≡1(mod N)
- 那么只要有一个b满足,必然导致一个a·b不满足,再加上一个a,使得至少有一半不满足
可以通过多测试几个a<N,来降低出错率
Largrange素数定理:令π(x)为≤x的素数的个数,则有π(x)≈x/(ln x),或者说
所以随机选定一个N,N是素数的概率至少有1/n
两类随机算法
蒙特卡洛算法:
- 运行时间有界
- 正确性随机
- 例子:素数测试
拉斯维加斯算法:
- 一直正确
- 运行时间随机
- 例子:快排、哈希
密码学
RSA机制:
性质:随机选取两个素数p、q,并令N=pq,对于任意与(p-1)(q-1)互素的整数e,有以下性质成立:
- 映射x→xe mod N是定义在集合{0,1,…,N-1}上的双向映射
- 另外,容易得到该映射的逆映射:令d为e mod (p-1)(q-1)的乘法逆元,则对于所有{0,1,…,N-1},
- 有(xe)d≡x mod N
发布者将(N,e)作为公钥,d作为私钥
Proof (xe)d≡x mod N:
- ed≡1 mod (p-1)(q-1) ⇒ ed= 1+ k(p-1)(q-1)
- 则有(xe)d-x=x1+k(p-1)(q-1)-x,可以被p整除,因为xp-1≡1 mod p,q同样,则必定被N=pq整除
分治算法
乘法
启发:
复数乘法中(a+bi)(c+di)=ac-bd+(bc+ad)i包含四次乘法,但实际可以通过计算ac、bd、(a+b)(c+d),因为bc+ad=(a+b)(c+d)-ac-bd,由4次减到3次,由此可以应用到常规乘法。
x=2n/2xL+xR;y=2n/2yL+yR;
xy=2nxLyL+2n/2(xLyR+xRyL)+xRyR
复杂度分析:T(n)=4T(n/2)+O(n),4次n/2位乘法+3次n位加法。O(n2)
继续化简,只需计算xLyL、xRyR、(xL+xR)(yL+yR),
修改后的复杂度为T(n)=3T(n/2)+O(n),3次n/2位乘法+3次n位加法。O(n1.59)
algo:
multiply(x,y)
if n=1 return xy;
xL,xR=leftmost[n/2],rightmost[n/2] bits of x
yL,yR=leftmost[n/2],rightmost[n/2] bits of y
P1=multiply(xL,yL)
P2=multiply(xR,yR)
P3=multiply(xL+xR,yL+yR)
return P1×2n+(P3-P1-P2)×2n/2+P2复杂度计算:
递归层数为log n,在第k层花费的总时间为
- k=0时,时间为O(n)
- k=log2 n时,时间为
- 在顶层和最底层之间,工作耗时呈等比数列(几何级数)增长,每增长因子为3/2
- 时间复杂度由底层决定,为
递推式、主定理
对于式子
有
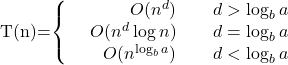
proof:
我们在第k层的时间复杂度可以表示为
总时间T(n)是上式对k从0到logbn求和,因为是等比数列,所以比例小于1取决于第一项(常数),等于1为对数,大于取决于最高次项
归并排序、逆序对
归并排序
algo:
function mergesort(a[1...n])
if n>1:
| return merge(mergesort(a[1...[n/2]]),mergesort(a[[n/2+1]...n]))
| else return a
function merge(x[1...k],y[1...l])
if k=0:return y
if l=0:return x
...继续递归或用循环merge的时间复杂度是O(k+l),mergesort的总时间复杂度是T(n)=2T(n/2)+O(n),或O(n log n)
计算逆序对
想法:
- 将数组分为左右两部分
- 分别计算两部分中的逆序对
- Combine:计算横跨两个部分的逆序对
第三步很难,但如果左右两部分有序,就可以通过两个指针分别移动,快速计算出逆序。与mergesort结合⇒Sort_and_Count
Sort_and_Count(L)
input:List L;
output:逆序对及排序
if L.size()=1 then
| return (0,L);
end
Divide L into A & B
(rA,A)←Sort_and_Count(A);
(rB,B)←Sort_and_Count(B);
(rAB,L)←Merge_and_Count(A,B);
return (rA+rB+rAB,L);时间复杂度是T(n)=2T(n/2)+Θ(n),或O(n log n)
中位数/选择问题
选择问题:选取数组中第k小的元素,中位数即k=[n/2]
完全排序可以得到,复杂度O(n log n),但做了多余的工作
算法:
- 随机选取一个标准v(同快排),将数组元素按和v的大小关系分成三组[SL]、v、[SR]
- 根据k在两个集合中继续寻找,或幸运地取到v
复杂度分析:
理想状态下有|SL|,|SR|≈1/2|S|,此时有T(n)=T(n/2)+O(n),线性时间
最差情况下有n+(n-1)+…+n/2=Θ(n2)
Lemma: 掷硬币时,第一次掷出字时,掷出次数的期望为2
Proof: 设期望为E,有E=1+1/2E ⇒ E=2
我们假定求中位数时一个“好”的选取落在1/4至3/4之间,因此在平均2次划分操作后,我们可以将数组大小由n缩减至3n/4,可得
T(n)≤T(3n/4)+O(n)(大小为3n/4的数组的运算时间 + n→3n/4的时间),可以得到一般情况下T(n)=O(n)
矩阵乘法
则有
借鉴乘法算法的思想,有
其中P1-8=…懒得敲了
T(n)=7T(n/2)+O(n2),
快速傅里叶变换
复数计算
z=a+bi=r(cosθ+i sinθ)=reiθ=(r,θ)
运算法则:
- -z=(r,θ+π)
- (r1,θ1)×(r2,θ2)=(r1r2,θ1+θ2)
- r=1时,zn=(1,nθ)
对于方程zn=1的解,可以写作{1,ω,ω2,…,ωn-1},其中ω=e2πi/n
当n是偶数时:
- 方程的解正负成对出现(1,θ)、(1,θ+π)同时出现
- 该方程解的平方,是zn/2=1的解
复共轭:z=reiθ,则z*=re-iθ
向量u=(u0,…,un-1),v=(v0,…,vn-1),两个向量的夹角为一个比例因子乘以两个向量的内积。注意在复数空间中内积的定义与实数空间不同,如下:
快速傅里叶变换FFT
问题描述:A(x)=a0+a1x+…+adxd,B(x)=b0+b1x+…+bdxd,如何求乘积C(x)=c0+c1x+…+c2dx2d,其中
可以观察到C(x)有2d+1个未知数,所以需要2d+1个方程才能解出
想法:
- 选取点集X={x0,x1,…,xn-1} ,n≥2d+1
- 计算A(X)和B(X)
- 计算C(X)=A(X)·B(X)
- 用n个C(X)解出2d+1个系数
简单分析,第二步计算一个值需要O(n),所以上界是Θ(n2),如何优化?
第二步优化:
- 选n个点{±x0,±x1,…,±xn/2-1}
- 将A(x)=Ae(x2)+xAo(x2),其中Ae是偶此项系数,Ao是奇次项系数
- A(xi)=Ae(xi2)+xAo(xi2); A(-xi)=Ae(xi2)-xAo(xi2)
- 应用递归,计算Ae(x)、Ao(x)同样进行分割
时间复杂度:T(n)=2T(n/2)+O(n),O(n log n)
为了能够递归,我们需要x2也两两正负配对,所以x选取zn=1的根
第四步优化:
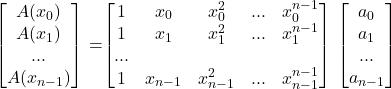
现在我们得到了上式中左边两个矩阵,显然如果大矩阵M可逆,那么解出系数非常容易。
观察发现M是范德蒙矩阵,对于范德蒙矩阵,如果x两两不同则可逆,再代入ω,得到
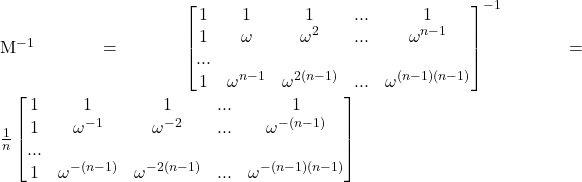
时间复杂度,对于一般的范德蒙矩阵,解逆矩阵O(n2),但我们使用了特殊的ω,列向量间彼此正交,则有MM*=nI,所以M-1=1/nM*,似乎是O(n),观察矩阵发现只有2n-1个数要算。在通过逆矩阵计算C的系数时,FFT继续进行了分治,将复杂度降低到了O(n log n),参见课本P79,我看不懂。
图算法
图的分解
无向图
DFS
DFS(G)
for all v ∈ V do
| visited(v) = false;
end
for all v ∈ V do
| if not visited(v) then Explore(G, v);
end
EXPLORE(G, v)
input : G = (V,E) is a graph; v ∈ V
output: visited(u) to true for all nodes u reachable from v visited(v) = true
PREVISIT(v);
for each edge (v,u) ∈ E do
| if not visited(u) then EXPLORE(G, u);
end
POSTVISIT(v);图的连通性
树边(tree edge):DFS时经过的边
回边(back edge):树边以外的边
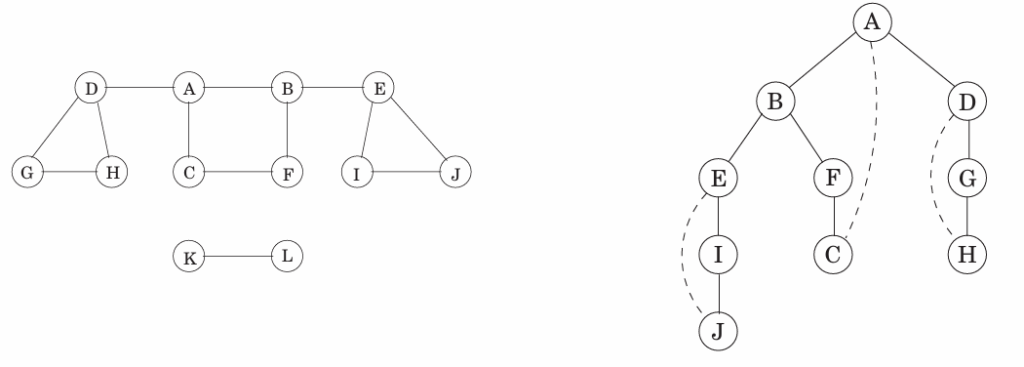
连通图:任意顶点间两两有路径的图
连通部件 /连通分量(connected component):原图的子图,且内部顶点两两间有路径。上图中{A,…,J}、{K,L}都是。
从某个顶点开始的DFS会找出顶点对应的连通部件;每调用一次Explore都会产生一个新的连通部件。
前序及后序
用pre[v]、post[v]表示顶点v第一次和最后一次被访问的时间,DFS结束后,会发现:
[pre[u], post[u]]、[pre[v],post[v]]或不相交,或一个包含另一个
有向图
DFS
DFS会生成搜索树/森林,产生树根、祖先后代、父子等概念
树边:DFS经过的边
前向边(forward edge):指向非子节点的后代
回边:指向祖先
横跨边(cross edge):去除掉前向边和回边后,从一个顶点指向另一个被完全访问过的边
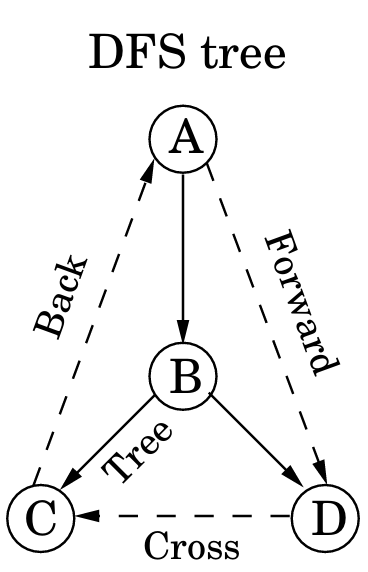
类比pre[v],post[v],可以用以下方法区分四种边
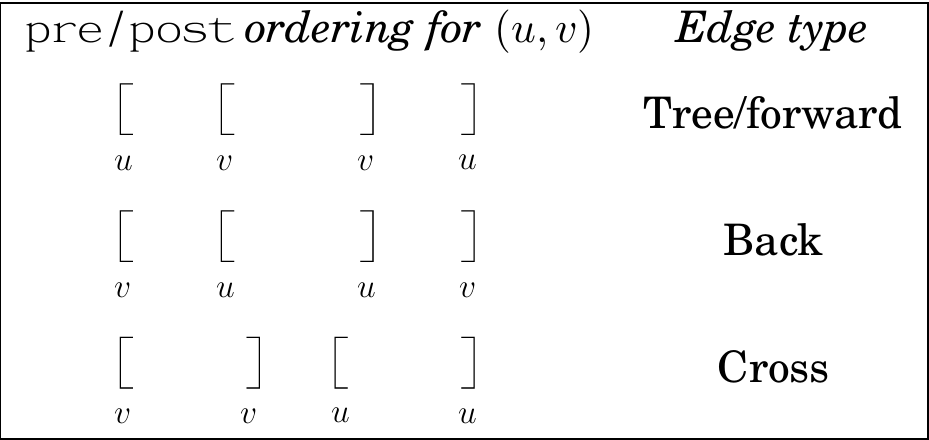
有向无环图DAG
Lemma: 有向图有环,当且仅当DFS有回边
线性/拓扑排序:所有有向无环图均有拓扑排序
DAG⇔DFS无回边⇔有拓扑排序
Lemma: DAG中,e(u,v),post[v]<post[u]
得出拓扑排序有O(n)的算法
源点(source):没有入边的点
汇点(sink):没有出边的点
Lemma: 每个DAG都有至少一个源点,至少一个汇点
强连通部件/分量
连通:uv之间存在u→v的路径,也存在v→u的路径,则uv连通
强连通分量(SCC):原图的子图,且内部顶点两两间连通。
源点强连通分量(source SCC):在“超图”(即b图)中,源点对应的强连通分量({A})
汇点强连通分量(sink SCC):在“超图”(即b图)中,汇点对应的强连通分量({D}和{G,H,I,J,K,L})
可以将图分为多个互不相交的SCC
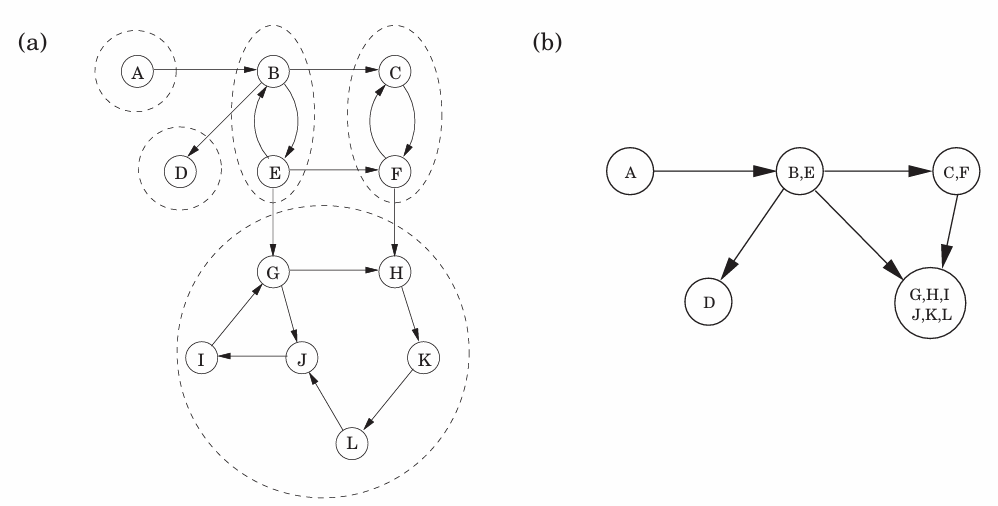
Lemma: 每个有向图关于其SCC是一个DAG,上图中左侧有环,右侧无环
求出强连通部件
Lemma1: DFS时,一次Explore从u点开始,那么该进程恰好会在 所有u可达的顶点v被访问后 停止
所以,如果顶点u在一个汇点强连通分量中,我们恰好能得到这个强连通分量。
问题:
- 如何找到处于汇点强连通分量中的顶点u
- 找到一个强连通分量之后怎么办
解决第一个问题:
Lemma2: C,C’是两个SCC,存在一条边C→C’,则C中最大的post[u]大于C’中最大的post[u]
Proof:拓扑排序
根据Lemma2可以得到下面的Lemma3
Lemma3: post[u]最大的u必定落在一个源点强连通分量中
考虑原图的反转图(reverse graph),即G中e(u,v)→G’中e(v,u),G’中的源点强连通分量恰好是G中汇点强连通分量,因此在G’中做DFS可以解决第一个问题。
解决第二个问题:
根据Lemma3,删除第一个SCC后,剩余的post[v]最大的顶点恰好落在G中下一个汇点强连通分量中,因此可以一直应用这条性质直到结束。
线性时间的算法:
- 在G’上做DFS
- 按上一步中post[v]降序的顺序,在G上运行DFS(访问过的不再Explore)
相关问题:
关键路径
ps:假设所有路径长度都为1
- 进行遍历,标记每个顶点的入度
- 完成入度为0的任务
- 更新一遍入度,重复步骤2-3直到结束
给定有向图,找到一顶点可以到达所有其他顶点
法1:
- 绘制“超图”
- 如果有多个源点强连通分量,则不存在;如果只有一个源点强连通分量,则这个SCC中的任意一个点都满足
法2:
- 调用DFS,找到post[u]最大的顶点u
- 从u开始DFS,如果访问了所有顶点,则满足条件
图中的路径
广度优先搜索BFS
距离:两顶点最短的路径长度
BFS(G, s)
input : Graph G = (V, E), directed or undirected; Vertex s ∈ V
output: For all vertices u reachable from s, dist(u) is the set to the distance from s to s
for all v ∈ V do
| dist(v) = ∞;
end
dist[s] = 0;
Q=[s] queue containing just v;
while Q is not empty do
| u=Eject(Q);
| for all edge (u,v) ∈ E do
| | if dist(v) = ∞then
| | | Inject(Q,v); dist[v] = dist[u] + 1;
| | end
| end
endBFS适用于每条边长度相等的情况,如果不等?
——可以将长度为n的点切分成n段长度为1的,但是时间复杂度极高
Dijkstra算法
DIJKSTRA(G, l, s)
input : Graph G = (V, E), directed or undirected; positive edge length {le | e ∈ E };Vertexs ∈ V
output: For all vertices u reachable from s, dist(u) is the set to the distance from s to u
for all u ∈ V do
| dist(u) = ∞;prev(u) = nil;
end
dist(s) = 0;
H =makequeue(V) \\using dist-values as keys;
while H is not empty do
| u=deletemin(H);
| for all edge (u, v) E do
| | if dist(v) > dist(u) + l(u, v) then
| | | dist(v) = dist(u) + l(u, v); prev(v) = u;
| | | decreasekey (H,v);
| | end
| end
end各种实现的时间复杂度:

证明Dijkstra的正确性
使用数学归纳法
S是已经确定dist的顶点集
base case:|S|=1,S={s},dist[s]=0
归纳假设:假设|S|>1时成立
- v是下一个添加到S的顶点,e(u,v)是最终选择的边
- dist(s,u)表示最终s→u的最短路径长度,令π(v)=dist(s,u)+l(u,v)
- 我们需要证明其他s→v的路径P长度比π(v)更长
- 如图假设存在这样一条路径P=P’+e+…
- 有 l(P)≥l(P’)+ le≥dist[x] + le≥π(y)≥π(v)
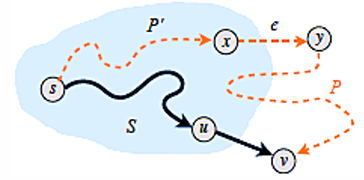
有负边无负环的最短路径——贝尔曼·福特算法
SHORTEST-PATHS(G, l, s)
input : Graph G = (V, E), edge length {le | e ∈ E}; Vertex s ∈ V
output: For all vertices u reachable from s, dist(u) is the set to the distance from s to u
for all u ∈ V do
| dist(u) = ∞;
end
dist[s] = 0;
repeat |V|- 1 times: for e ∈ E do//因为最多经过|V|- 1条边,即把每个点走一遍
| UPDATE(e);
end
UPDATE(e):dist(v)=min{dist(v),dist(u)+l(u,v)}//只会更新dist(u)存在的点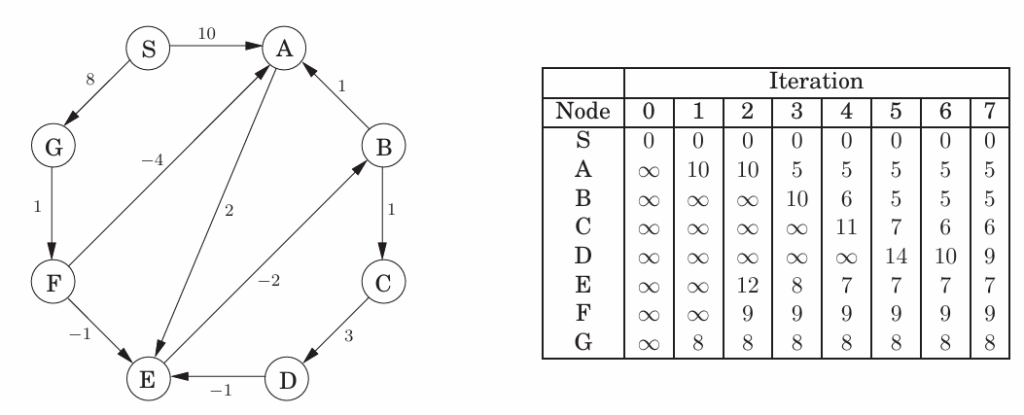
问题:负环的出现使得路径无意义
解决:在|V|-1轮以后再进行一轮,如果有值变化则存在负环
有向无环图DAG的最短路径
注意到:在DAG的任意路径中,顶点按拓扑序出现
DAG-SHORTEST-PATHS(G, l, s)
input : Graph G = (V, E), edge length le e ∈ E ; Vertex s ∈ V
output: For all vertices u reachable from s, dist(u) is the set to the distance from s to u
for all u ∈ V do
| dist(u) = ∞;
end
dist[s] = 0;
linearize G;
for each v ∈ V\{s} , in linearized order do
| dist(v) = min(u,v)∈E {dist(u) + l(u,v)};
end允许负边存在
求最长路径:将所有边长取负
贪心算法
最小生成树MST
引理
Lemma1: 去除一条在环中的边不会改变图的连通性
Lemma2: n个节点的树有n-1条边
- 初始只有n个节点,加边;加边时或连接两个部件,使得部件数-1;或连接同一个部件中的两个顶点,导致成环,舍去
Lemma3: 任何连通的无向图,如果|E|=|V|-1,必是一棵树
- 如果有环就去掉一条边,得到G‘=(V,E’),由Lemma1可知不会影响连通性
- 任取一个连通的无向图G
- 因为无环,所以G’是一棵树,于是|E’|=|V|-1
- 所以如果有|E|=|V|-1,E=E’,G=G’,G是一棵树
Lemma4: 无向图中,如果节点间路径唯一,则是一棵树
- 如果有两条路径,必成环
割定理Cut Property
X是图G最小生成树MST的一部分,X包含两部分互不连通的集合S,V\S,e是S→V\S中最短的边,则X∪{e}是图G最小生成树的一部分
证明:
- 假设有一条更长的边e’,最小生成树为T,T’=T+{e’}\{e}
- weight(T’)=weight(T)+w(e’)-w(e)>weight(T)
- 显然不选择最短边e的树T‘不是最小生成树
Kruskal算法
- 将所有边按权值升序排列
- 按顺序遍历所有边,添加到图中,如果成环舍去
algo:
KRUSKAL(G, w)
input : A connected undirected graph G = (V, E), with edge weight we
output: A minimum spanning tree defined by the edges X
for all u ∈ V do
| makeset (u);
end
X = { };
Sort the edges E by weight;
for all (u, v) E in increasing order of weight do
| if find (u)≠find (v) then
| | add (u, v) to X;
| | union (u,v)
| end
end使用的数据结构:不相交集
- makeset(x): create a singleton set containing x; |V|
- find(x): find the set that x belong to; 2·|E|
- union(x, y): merge the sets containing x and y; |V| – 1
Prim算法
假设AB两部分分别有两颗最小生成树S,T,选取A→B最短边e,S∪T∪e是整体的最小生成树
仿照Dijkstra算法,保证拥有一颗最小生成树S,然后不断添加e
algo:
PRIM(G, w)
input : A connected undirected graph G = (V, E), with edge weights we
output: A minimum spanning tree defined by the array prev
for all u ∈ V do
| cost(u) = ∞;
| prev(u) = nil;
end
pick any initial node u0;
cost(u0) = 0;
H =makequeue(V) using cost-values as keys;
while H is not empty do
| v=deletemin(H);
| for each (v, z) ∈ E do
| | if cost(z) > w(v, z) then
| | | cost(v) = w(v, z); prev(z) = v;
| | | decreasekey (H,z);
| | end
| end
end红蓝染色算法
- 在环中将最长边染红(每个环都产生一颗最小生成树,实际将图分成了多个MST和多个孤立的点)
- 在MST和点中任选两个,将两部分间最短的边染蓝,直到只剩一部分
- 蓝边即为MST
集合覆盖
问题描述:
- 输入:集合B,集合B的子集S1,S2,…,Sm
- 输出:一系列Si,Si的并集是B
- cost:Si的数量
贪心算法:每次添加一个包含未被覆盖元素最多的Si
Lemma: 假设最优解需要OPT个集合,那么贪心算法至多需要ln n·OPT个集合,n为|B|
Proof:
- 假设到第t次迭代仍有nt个元素未被覆盖(n0=n)
- 因为所有元素可以用OPT个集合覆盖,所以贪心算法至少可以找到一个包含nt/OPT个未覆盖元素的集合(假设我们现在想找出a个元素的覆盖,那么最差情况就是a个元素被平均分配到OPT个集合中,每个集合中包含a/OPT个所需元素)
- 这就意味着nt+1≤nt(1-1/OPT)
- nt≤n0(1-1/OPT)t<n0(e-1/OPT)t=ne-t/OPT(应用1-x≤e-x)
- 我们的目标是nt=0,也就需要ne-t/OPT=1,t=ln n·OPT
找零问题
目标:用最少的钱数找零
Cashier’s algorithm:每次选一张面额最大的钱,显然对于某些面额不总是得到最优解,但我们可以证明对于某些面额总能得到最优解。
证明在USD的面额{1,5,10,25,100}中,贪心算法总能得到最优解
我们需要证明在任意一个最优解中,至多有4张$1,1张$5……
- 假设我们需要付x元,ck≤x<ck+1
- 需要证明所有的最优解都会选择ck而不是用{c1,…,ck-1}凑出x,下面的表格证明了这一点(真证了吗?似乎只能靠归纳+遍历证明)。比如我们要证明在5-9这一段必须取一张5,就采用反证法,假设我们用n张一元得到了最优解,然后用1张5元替换掉,得到一个更优的解,与假设矛盾;同样,在证明10-24这段必须取10时,我们就通过将两张5元替换成1张10元的方式(理论上我们在第一轮已经证明了在金额大于等于5的情况下,5元都比1元更优,所以我们不用考虑用10元替换1*5+5*1或1*10的情况),继续证明

动态规划
回忆:有向无环图中的最短路径
for循环在解决子问题{dist(u): u∈V},最初的子问题是dist(s)=0,然后逐渐解决一个更大的子问题
最长递增子序列
问题描述:给出序列a1,…,an,给出一个有序的子序列ai1,ai2,…,aik,其中1≤i1<i2<…<ik≤n,使k最大。如:

算法:
- 按大小关系构建DAG
- 找最长路径
- 第一种方式在DAG的最短路径问题中写过
- 另一种方法:
实际就是第一种方法把min改成maxfor j=1 to n do
| L(j)=1+max{L(i)|(i,j)∈E};
end
return maxjL(j));
两种算法的时间复杂度都是O(n2),因为构建DAG就是O(n2),循环最差也是O(n2)
事实上L(j)=1+max{L(i)|(i,j)∈E};可以用一个递归程序解决,但是使用递归会导致复杂度变成指数
编辑距离
问题描述:将两个字符串通过添加空格和修改的方法对齐,最少需要几个空格和修改

对于原问题构建子问题
- 假设字符串x,y的长度为m,n,E(i,j)表示x[1…i],y[1…j]时的编辑距离
- E(i,j)的取值无非三种
- 仅x变长,y增加一个空格:1+E(i-1,j)
- 仅y变长,x增加一个空格:1+E(i,j-1)
- xy同时变长:diff(i,j)+E(i-1,j-1) 我们让E(i,j)在三种情况中取最小即可
例:求EXPONENTIAL和POLYNOMIAL的编辑距离时,解子问题E(4,3),前缀EXPO和POL,对应三种取值
事实上,编辑距离的计算可以看成填写下面这样的表格
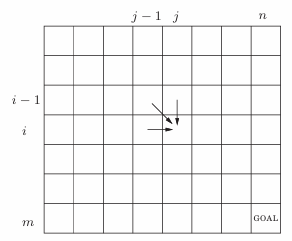
algo:
for i = 0 to m do
| E(i,0) = i;
end
for j = 1 to n do
| E(0,j) = j;
end
for i = 1 to m do
| for j = 1 to n do
| | E(i,j) = min{1+E(i-1,j),1+E(i,j-1),diff(i,j)+E(i-1,j-1)};
| end
end
return(E(m,n));
diff(i,j)
return x[i]==y[j]填了一个m·n的表,时间复杂度O(m·n)空间也是O(m·n)
空间可优化:因为填表是一行一行填,我们只需要保存上一行就行
时间可优化:按左上、右下分治
动态规划问题中经常需要填表,根据表的大小、前项依赖关系,可以得出时间复杂度

背包问题
问题描述:背包容量W,物品有n种,物品i有价值v[i]和体积w[i],物品个数无限,如何装价值最高?
构建子问题:
algo:
K(0) = 0;
for w = 1to W do
| K(w) =maxi:w[i]≤w{K(w-w[i])+v[i]};
end
return(K(W));时间复杂度:O(n·W)
如果个数只有1个?
algo:
Initialize all K(0,j) = 0 and all K(w,0) = 0;
for w = 1 to W do//求出容量为w时的最大价值
| for j = 1 to n do//求出只有前j个物品时的最大值
| | if wj > w then K(w,j) = K(w,j-1);
| | K(w,j) =max{K(w-wj,j-1)+vj,K(w,j-1)};//在重量为w-wj的基础上放入第j个物品或不放入
| end
end
return(K(W,n));时间复杂度:O(n·W)
最长公共子序列LCS
问题描述:给定x[1,…,m],y[1,…,n],分别删除x,y的一部分,使得剩下的字符串相同,这个字符串最长是什么
例:LCS(GGCACCACG, ACGGCGGATACG ) = GGCAACG
![Rendered by QuickLaTeX.com LCS[i,j]=\left\{\begin{array}{lr}& 0\\& LCS[i-1,j-1]+1\\&max\{LCS[i-1,j],LCS[i,j-1]\}\\\end{array}\right.\begin{array}{lr}& if\quad i=0 \vee j=0\\& if\quad a[i]==b[j]\\& otherwise\\\end{array}](https://www.smzytyzg.tw.cn/wp-content/ql-cache/quicklatex.com-d7f10b2db3bab1f65b7a5b713e5cf0d3_l3.png)
相关问题:最长公共子串
![Rendered by QuickLaTeX.com LCS[i,j]=\left\{\begin{array}{lr}& 0\\& LCS[i-1,j-1]+1\\&0\\\end{array}\right.\begin{array}{lr}& if\quad i=0 \vee j=0\\& if\quad a[i]==b[j]\\& otherwise\\\end{array}](https://www.smzytyzg.tw.cn/wp-content/ql-cache/quicklatex.com-af357cc187ce9f411d4118743164ed7e_l3.png)
矩阵连乘
计算如A·B·C·D的矩阵乘法时,应用结合律可以很好的降低复杂度,别的没讲,填一个三维表,O(n3)
三分问题
问题描述:给定整数集合{𝑎1,𝑎2,…,𝑎𝑛},判断是否可以将其分割为三个相互不相交的子集𝐼,𝐽,𝐾,使得
四维表P(i,x,y,z),表示前i个数字,x+y+z是否等于前i个数字的和
递推式:P(i,x,y,z)=P(i-1,x-ai,y,z)∨P(i-1,x,y-ai,z)∨P(i-1,x,y,z-ai)
出口:P(1,a1,0,0)=P(1,0,a1,0)=P(1,0,0,a1)=True
求P(n,s/3,s/3,s/3)
最短可靠路径
问题描述:求两点间最短路径,但限制最多经过k个节点
F(i,v) 表示经过i个节点到达v节点的的最短路径
递推式:F(i,v)=min{mine(u,v)∈E{F(i-1,u)+l(u,v)},F(i-1,v)}
内层min表示表示求恰好经过i个节点的最短路径,外层min表示可以经过比i小个节点
使用瞪眼法,可以发现恰好是贝尔曼·福特算法填表的前k列
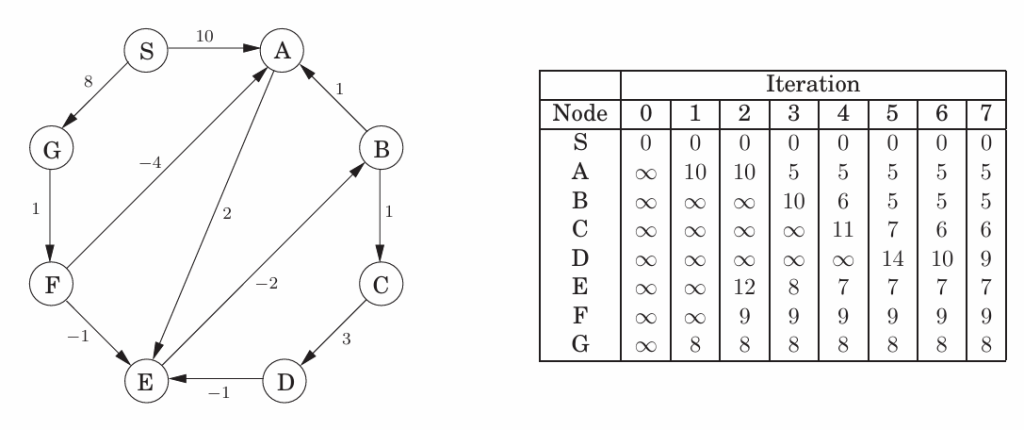
多源最短路径All-pairs shortest path
问题描述:得出图中任意两个顶点间的最短路径
显然,我们可以在每个节点上做一次贝尔曼福特算法,复杂度O(|V|2|E|),因为点一般比边少,所以目标是O(|V|3)
Floyd-Warshall算法
将顶点编号1…n
用dist(u,v,k)表示u,v两点间,只使用前k个顶点的最短距离
递推式:dist(u,v,k)=min{dist(u,v,k-1), dist(u,k,k-1)+dist(k,v,k-1)}//注意k在前两个变量时表示第k个顶点
algo:
for i = 1 to n do
| for j = 1 to n do
| | dist(i, j, 0) = ∞;
| end
end
for all (i,j) ∈ E do
| dist(i, j, 0) = l(i,j);
end
for k = 1 to n do
| for i = 1 to n do
| | for j = 1 to n do
| | | dist(i, j, k) = min{dist(i,j,k − 1),dist(i,k,k − 1) + dist(k,j,k − 1)};
| | end
| end
end旅行商人问题TSP
问题描述:如何用最短的路径访问所有顶点(访问且仅访问一遍)并返回起点。每两个顶点间均存在路径
将顶点编号1….n,规定从1号顶点开始
用S表示包含1号顶点的V的子集,用C(S,j)表示从1出发,访问S中所有顶点(不返回1),最终停在顶点j的最短路径长度
递推式:C(S,j)=mini∈S,i≠j{C(S\{j},i)+dist(i,j)}
algo:
C(1,1) = 0;
for s = 2 to n do
| for all subsets S ⊆ {1,2,...,n} do//按|S|递增顺序
| | C(S,1) = ∞;
| | for all j ∈ S and j= 1 do
| | | C(S,j) = mini∈S:i≠j C(S\{j},i) + dij;
| | end
| end
end
return(minj C({1,2,...,n},j) + dj1);复杂度分析:2n·n个子问题,每个运行线性时间,O(n2·2n)
树中独立集
问题描述:
独立集:图中选取顶点,两两间没有边
在一颗树中找出最大的独立集
用I(u)表示u及其子树上的最大独立集
递推式:
线性规划
线性规划问题的定义:给定一系列变量,给变量赋值,使得变量的值满足一系列等式及不等式,并使目标函数最大化/最小化
除了Infeasible(不存在可解空间)和Unbounded(可解空间无边界,这种情况也可能在顶点上)两种情况,线性规划的最优解都在顶点上
浅谈单纯形法Simplex Method
爬山法。在多边形的顶点上,移动到值更优的邻居,直到没有邻居比自己更优。
问题:怎么解出顶点;怎么确定邻居
顶点:二维两个不等式取等号的点;n维:n个不等式取等号的点。可能出现在可解空间外,去除即可
邻居:n维情况下,两个顶点中n个顶点只有1个不同。但是一个顶点可能有n+1个等式取等,引发“退化”问题
整数线性规划
如果顶点坐标不是整数(包括使用变换之后),而我们依然要求找到最优的整数解,那么没有多项式时间算法
对偶问题
注意maxmize→minimize
原问题:

令:
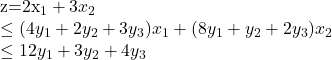
不等号在
时满足
对偶问题:
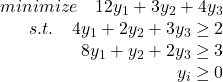
原问题:
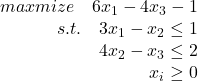
令:
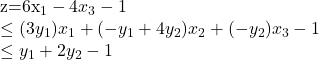
不等号在
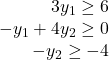
时满足
对偶问题:

Theorem:如果原线性规划有有界(bounded)最优值,那么对偶问题也有有界最优值,且两个最优值重合
对偶的应用:
1.将两个不相关的问题联系起来(最大流→最小割)
2.假设我们通过单纯形法得到了一个顶点,我们如何确定他是哪几个不等式取等号得到的?
——对偶问题中不为0的yi对应原问题第i个不等式取等
最短路径
Dijkstra算法的线性规划形式

边界收缩,增加dt来找到边界
从最短路径问题出发
将图割成S、T两部分,其中s点在S,t点在T;将这个割写作S,δ(S)是S经过的所有边的集合;所有符合条件的割S的集合写作C。最短路径问题可以用下面的整数线性规划问题描述
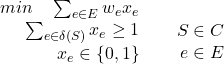
第一个不等式保证了在取任意一个割的时候,都会有至少一条边被穿过,也就保证了路径连续
目标函数保证了dist最小
优化:
- 将xe∈{0,1}修改为0≤xe≤1:因为最优值都在整数点,所以可以
- 进一步,直接0≤xe:因为min保证了最优值靠近原点,所以可以不用≤1
最终形式:

取对偶:
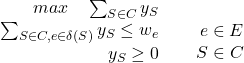
对应Moat(护城河)问题:在从s到t间筑造护城河,使得护城河宽度最宽
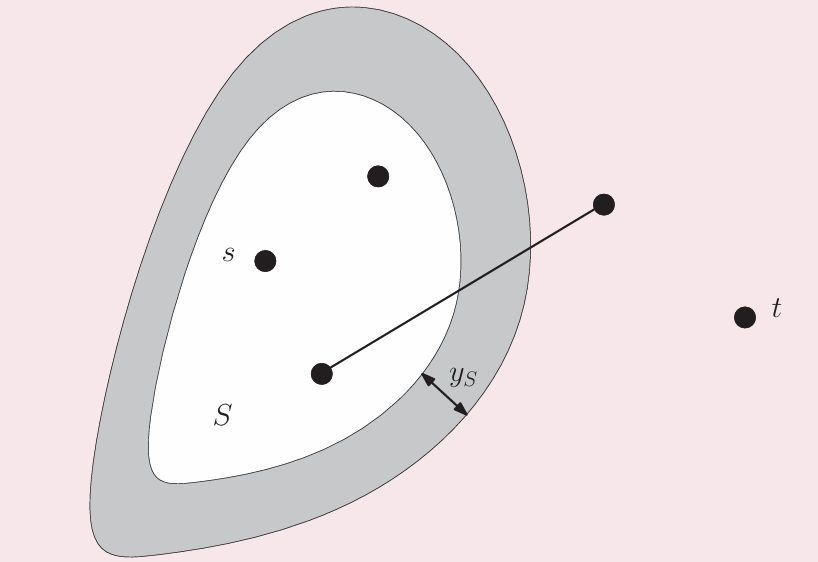
线性规划标准型
线性规划问题多种多样:max/min;等式/不等式;变量非负/任意;希望转换成一种标准格式,然后用一种方式解决
转换方式:
- max↔min:*-1
- 等式ax=b→不等式ax≥b,ax≤b;不等式ax>b→等式ax+s=b;s>0
- 负数→正数:定义x+和x–,x+和x–均非负,x替换成x+-x–
定义线性规划标准型:
- 变量非负
- 等式
- minimize
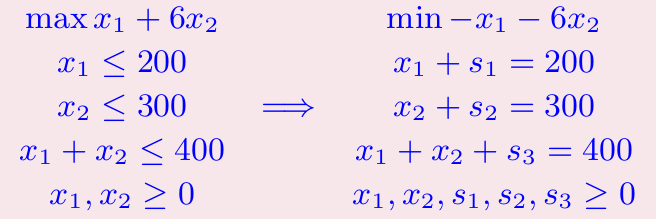
单纯形法算法Simplex Algorithm
Simplex:v是一个顶点,v‘是其邻居,v’有更好的value,则令v=v‘
顶点:某些超平面(线、面、超平面)相交的唯一的点(避免面面成线,所以强调唯一)
选取一些不等式,如果恰有一个点使这些不等式取等,那么这个点是顶点
邻居:n维空间中,如果两个顶点取等的不等式中有n-1个相同,则两点为邻居
算法:
- 在每次迭代中
- 从原点开始,检查邻居是否有更优的值,如果自己是最优的,则停止
- 如果有则移动过去
- 把坐标系原点移到当前点
为什么每次都要从原点开始?
- 如果目标函数中所有变量的系数都是负的(当我们一直移动到原点,最终目标函数会变成这样),那么原点就是最优值。(如maxmize -x1-3x2+5,最优值就是5)
- 当变量都为0时,我们可以很方便地找到邻居(如x1+2x2≤4,则邻居为(4,0) ,(0,2))
对线性规划进行坐标变换
从(0,0)开始增加x2,我们发现下一个触碰到的不等式是-x1+x2≤3,即找到一个邻居(0,3)
令y1=x1,y2=3+x1-x2≥0(注意新变量一定要≥0),可以将左边的原问题通过坐标变换变为右边的新问题

重复上面的步骤,我们增加y1,得到新邻居(1,0)
令z1=3-3y1+2y2,z2=y2,再得到新问题,可以发现目标函数中系数都为负,最优值是22

如何找到第一个顶点

我们可以通过上面这种方式,在原问题基础上找到一个新问题,新问题很容易找到一个顶点:xi=0;sj=0;z1=200,z2=300,z3=400
在这个顶点基础上解出线性规划,最优值显然会在zk=0时取到(如果取不到显然原问题infeasible),那么就会得到一个原问题的顶点
解决问题
退化问题
问题描述:n维空间,同一个点有大于n个不等式取等号,会导致顶点的邻居是其自己
解决方法:加个小扰动
Unbounded问题
问题描述:进行坐标变换时,发现永远不会碰到不等式,导致值一直增加
解决方法:设定一个max值,越界报错
时间复杂度
给定n个变量,m个约束(不包含xi≥0),最差情况下我们需要访问每个顶点,顶点个数为
是指数级的算法,但是在实际表现上很好
最大流最小割问题
问题描述:
- 最大流:有向图,每条边有最大流量,问从s到t的最大流量是多少
- 最小割:有向图,每条边有权值,用一个割将s和t分开,切割的最小权值是多少
最大流问题可以用下面的线性规划问题描述:
最大流问题
假定边e(i,j)的最大流量为cij,实际流量为fij
一般形式:最大化流,流量小于最大流量,流入等于流出
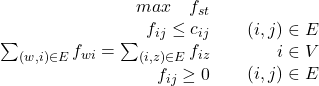
另一种形式:加一条t到s的边,容量∞,同样max流量,可以将=改为≤(方便求对偶),因为是一个环,f1≤f2≤…≤fn≤f1,注意E包含e(t,s)
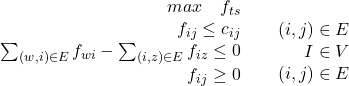
福特·福克森算法
- 从所有边流量为零开始
- 找到一条从s到t的路径,使流量尽可能大
- 因为我们需要有将一个流“取消”能力,所以如果在第二步中占用了边(u,v)上f的流量,就添加一条(v,u)上容量为f的新边
- 重复做2和3,直到找不到一条s到t的路径
例:
原图:
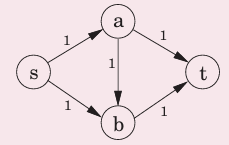
找到路径sabt,
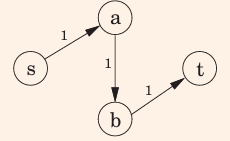
找到路径sbat,使用了上一步添加的e(b,a)
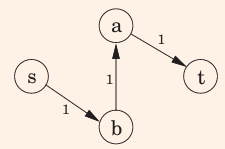
最终结果:
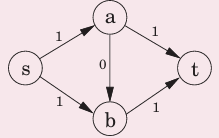
最小割问题
Theorem:网络中最大流的值等于最小割的值
Proof:假设最大流得出的流为f,则在剩余图G’中不存在s到t的路径,意味着图被分为LR两部分,size(f)=L→R的容量,且不存在R→L的流量;而其他的割势必会切到G‘中的边而使权值增大,因此最大流问题的瓶颈就是最小割的解
时间复杂度
DFS/BFS需要O(|E|)的时间来找到一条s-t的路径,假设最大流的值是C,我们最差每次可以增加1,所以时间复杂度是O(C|E|)(任意坏的)
优化:Edmonds-Karp算法,使用BFS,找到边最少的路径,迭代次数至多O(|V|·|E|),时间复杂度O(|V|·|E|2)
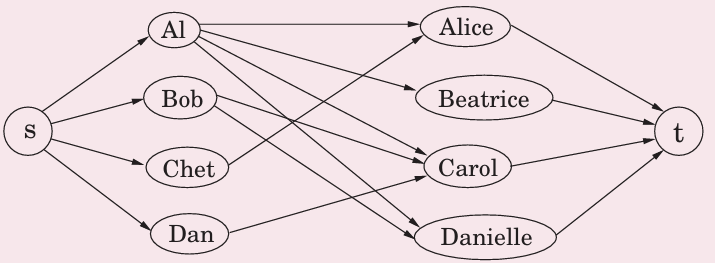
二分匹配
问题描述:使尽可能多的男孩、女孩匹配
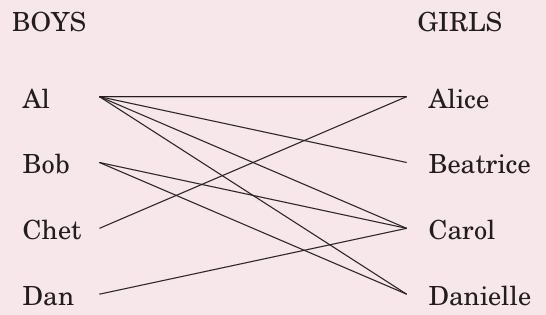
增加s,t,归约到最大流问题
NP问题
高效问题、困难问题、搜索问题
定义:
高效问题:在多项式时间内可解
困难问题:多项式时间内不可解
搜索问题:多项式时间内可验证一组解是否为此问题的解
是否存在困难问题,无论如何也无法变成高效问题?
高效问题和对应的困难问题:
最小生成树MST、旅行商人问题TSP
最小生成树问题:一般情况下,我们有多项式时间算法,但如果我们不允许最小生成树有分支(即找一条访问且仅访问一次所有顶点的最短路径,TSP问题),目前不存在多项式时间算法
旅行商人问题TSP
搜索问题描述:在带权值的全连接无向图中,找到一条路径:经过所有顶点且仅经过一次,再返回起点,总权值小于k;如果给出一条路径,显然多项式时间内可验证其权值小于k
优化问题描述:在全连接图中,找到一条最短路径:经过所有顶点且仅经过一次,再返回起点;
搜索问题与优化问题可在多项式时间内转化(可以互相规约)。
- 搜索→优化:优化问题找到一个解,放到搜索问题中验证
- 优化→搜索:二分查找,逐渐缩小k
2-SAT、SAT
SAT问题:给出一个CNF的可满足性,目前没有多项式时间算法。2-SAT问题限制每条子句中只含有两个变量,有多项式时间算法(Ex.3.28 in hw2)。甚至3-SAT也没有多项式时间算法
欧拉路径、Rudrata环/汉密尔顿环
欧拉路径
问题描述:给出一条路径,经过图中所有边,且仅经过一次
当且仅当,度为奇数的点有0/2个时有解
算法:欧拉路径去掉一个环还是欧拉路径,所以只需找到环,删去,再找环,最后把环拼起来。有多项式时间算法
Rudrata环/汉密尔顿环
问题描述:
原问题:在方格中,按马走日的走法,是否能将所有格子走且近走一次
图论中:在一个图中,是否能找到一个环路,经过所有顶点且仅经过一次(注意与TSP区分,这个没权重,不是完全图)
没有多项式时间算法
最小割、平衡割
最小割
问题描述:给定一个图,去掉最少的边,使这个图不连接(注意不是“最大流最小割”的那个“最小割”)
固定一个t,其他|V|-1个顶点做s,每条边容量为1,跑|V|-1次最大流,多项式时间
平衡割
问题描述:给定一个图,去掉最少的边,使这个图不连接,但是规定两部分顶点个数不能小于|V|/3,无多项式时间算法
线性规划、整数线性规划、0/1方程组
线性规划有多项式时间算法(单纯形法是指数),但整数线性规划没有多项式时间算法
ZOE:0/1方程组:方程组中系数为Ax=b,A中系数0/1,b为0/1,x的解为0/1,也是整数线性规划,没有多项式时间算法
匹配问题
2D匹配有多项式时间算法,3D没有
最大独立集、最小顶点覆盖、最大团
问题描述:
最大独立集:在图中找到一组顶点,两两间无边,使此独立集最大化
最小顶点覆盖:在图中找到一组顶点,使得每条边都至少有1个顶点被覆盖,使此顶点覆盖最小化
最大团:在图中找到一组顶点,使得顶点间两两有边(区分强连通分量SCC,SCC只要求两两间有路径),使此集合最大化
三个问题实际上是一个问题,可以互相规约
独立集⇔团:原图中两两无边的独立集,对应补图中两两有边的团
独立集⇔顶点覆盖:假设最大独立集S,则V\S为最小顶点覆盖(V\S中所有顶点都与S相连)
无多项式时间算法
最长路径
问题描述:从s到t的不含环的最长路径,无多项式时间算法
背包问题、子集和
背包问题
无论物品是否可重复,对于背包问题我们有O(nW)的算法,但是一般我们认为n和W都很大,我们使用n和W的数位长度作为输入,所以是指数级算法
在使用1进制时(数位长度等于数位大小,5写作11111),背包问题是一个多项式时间算法
子集和问题
给定值w和集合A,从A中选出某些值ai,使得
我们可以写作
是ZOE,没有多项式时间算法
P、NP问题
集合覆盖问题
问题描述:输入集合B,和B的一些子集S1,S2…Sm;输出选择的Si,其并集为B,使选择的Si数量最小
顶点覆盖是一个特殊的集合覆盖,在顶点在集合中出现且仅出现2次的情况下。(将顶点覆盖归约到了集合覆盖上)
图同构
判断两个图是否一致(边和顶点都一致),目前没有多项式时间算法
P、NP
P问题:给定一个问题,能在多项式时间内给出其一个解,如果不存在解也在多项式时间内停止
NP问题:给定一个问题,和一个可能的解,在多项式时间内验证这个解是否为这个问题的解
补问题:原问题回答T/F,补问题回答F/T(是否存在→是否不存在),表示为co
封闭:原问题和补问题属于同一类问题
P问题在补问题下是否封闭:显然,封闭P=co-P
NP问题在补问题下是否封闭:不封闭
几种猜想,目前是右下角,学者倾向于左下是正确的,左上角是P=NP
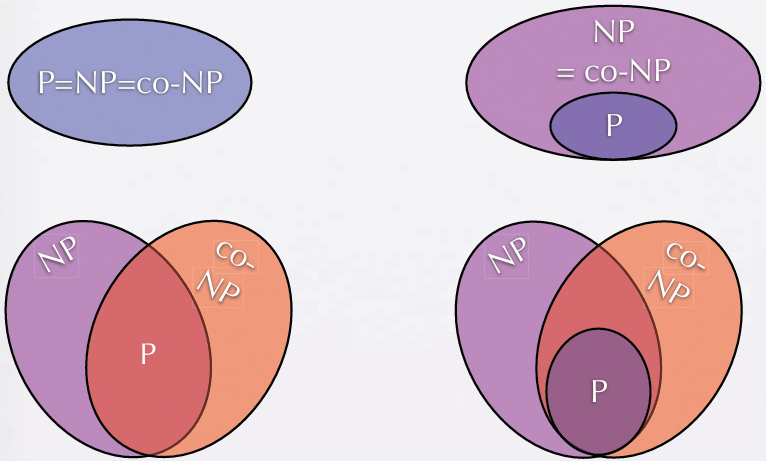
为什么倾向于P≠NP
如果P=NP,我们有多项式时间的方法证明任何一个问题
如果P≠NP,是否能找到一个必然需要多项式时间的问题?
——我们能够通过规约,将上面所有的难问题,归约到一个最难的NP问题;如果我们找到了这个最难的NP的多项式时间算法,那么可以在多项式时间内解决所有的NP问题
浅谈规约

将A规约到B的一个特殊情况,然后解决B,我们也就得到了一个A的解
注意是A比B简单(至少在描述上是简单的)
规约的三个用法:必考必出错
- 解决:将一个未知问题归约到一个已知问题,已知问题有一个算法,则我们得到一个未知问题的算法
- 证明:将一个已知问题归约到一个未知问题,我们可以证明未知问题比已知问题难
评估:将一个未知问题归约到一个已知问题,我们可以估计未知问题的难度
一般情况下,证明和评估只取其一,即两个问题无法互相规约,否则就是一个问题
NP-完全问题
NP-完全问题:所有NP问题都能规约到的问题,即最难的NP问题
如果我们找到一个NP-完全问题的多项式时间算法,我们可以在多项式时间内解决所有NP问题,那么P=NP
co-NP完备问题:所有的co-NP问题都能归约到的问题
一个问题是NP完备问题,当且仅当他的补问题是co-NP完备问题
如果所有NP问题的补问题都是NP-完备问题,那么co-NP=NP
永真式(tautology):一个CNF不可满足,当且仅当其否定永真;CNF的否定可以转换成DNF;DNF是永真式,当且仅当CNF的否定是永真式。
永真式是SAT问题的补问题
如果永真式是P问题,则SAT问题是P问题
如果永真式是NP问题,则co-NP=NP
一般认为因式分解问题(将一个整数分成质数的幂)不是NP-完备问题,因为因式分解问题在量子计算中有多项式时间算法,而其他NP-完备问题在量子计算时仍然没有多项式时间算法
质数合数问题互为补问题,没有多项式时间算法
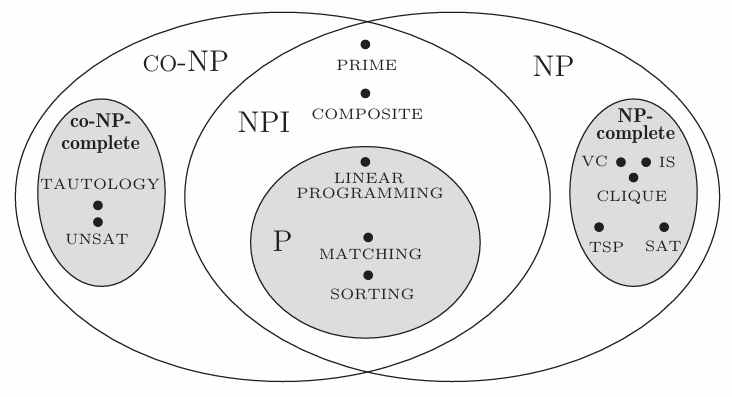
*注:NPI是NP-intermediate,定义是属于NP,但不属于P问题和NP-完备问题的问题
若P≠NP,则NPI非空
规约
回忆:规约的三个用法:
- 解决:将一个未知问题归约到一个已知问题,已知问题有一个算法,则我们得到一个位置问题的算法
- 证明:将一个已知问题归约到一个未知问题,我们可以证明未知问题比已知问题难(考这个)
评估:将一个未知问题归约到一个已知问题,我们可以估计未知问题的难度
规约路径(不唯一):
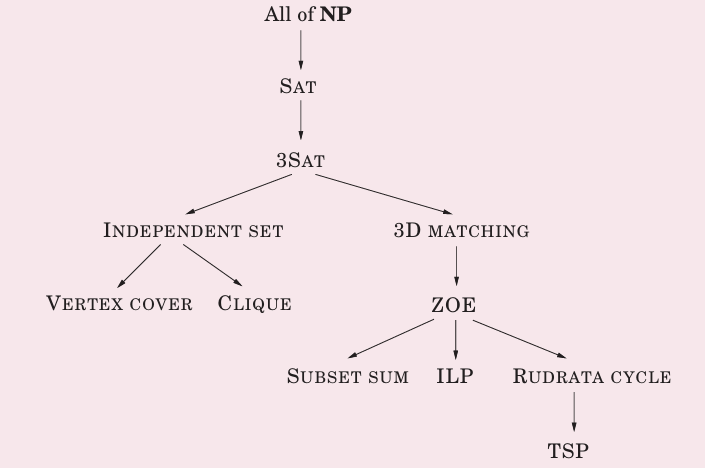
SAT问题是第一个NP-完备问题,也是NP-完备问题中最容易的问题
汉密尔顿路径→汉密尔顿环
问题描述:
- 汉密尔顿路径:给定两个点s,t,找到一条从s到t的路径,经过所有顶点且仅经过一次
- 汉密尔顿环:在一个图中,找到一个环路,经过所有顶点且仅经过一次
如何将汉密尔顿路径问题归约到汉密尔顿环问题:补充一个点,仅和s,t两点连接,在此点上调用汉密尔顿环,则可以得到一条从s到t的汉密尔顿路径
3-SAT→最大独立集
3-SAT:给出一个CNF的可满足性,这个CNF中每个语句里最多包含三个变量
最大独立集:在图中找出一个最大的集合,这个集合中元素两两无边
- 将3-SAT中的每个语句写成一个三角形,顶点两两相连
- 将不同三角形间,将一个值与其相反取值相连
- 假设原来有m个子句,则在图上找一个大小为m的独立集
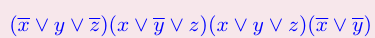
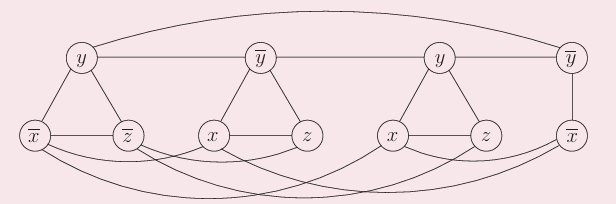
独立集中的每个点,都意味着一条语句为真,而我们又避免了一个值与其相反的取值同时被选取
SAT→3-SAT
我们只需要将SAT中变量数多于3的语句拆分
两个式子的可满足性相同(记得证两边)
为了在硬件上求解3-SAT问题,我们需要限制每个变量只出现3次以下(仍然是一个困难问题,但可以用硬件解决)。如果变量x出现在三个以上的子句中,我们可以将其替换为x1x2…xn,然后添加下面的语句,这个语句可以保证xi的取值一致
最大独立集→最小顶点覆盖、最大独立集→最大团
3-SAT→3D匹配
3D匹配:有n个男孩、n个女孩、和n个宠物,我们希望尽可能满足多的需求
根据不同的需求,我们可以将每个组合表示成一个三元组triple
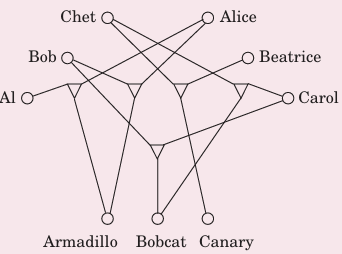
我们考虑3D匹配的一个子问题,强制两个男孩b0b1、两个女孩g0g1只出现在这四个triple中(四个宠物显然会出现在其他地方,否则就无解了),我们取出这四个triple,作为一个元
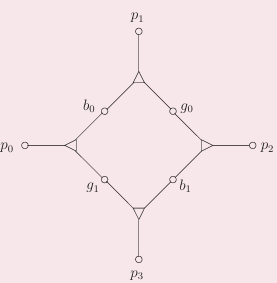
我们可以发现,四个triple只有两个能同时满足(左右两个或上下两个)
我们可以将这个元看成一个硬件,四个引脚的值的关系:p0=p2=¬p1=¬p3
不同的元会出现相同的宠物,我们将宠物用非门连接,如下图,假定我们给p0输入一个高电平,可以对应得出其他引脚的值
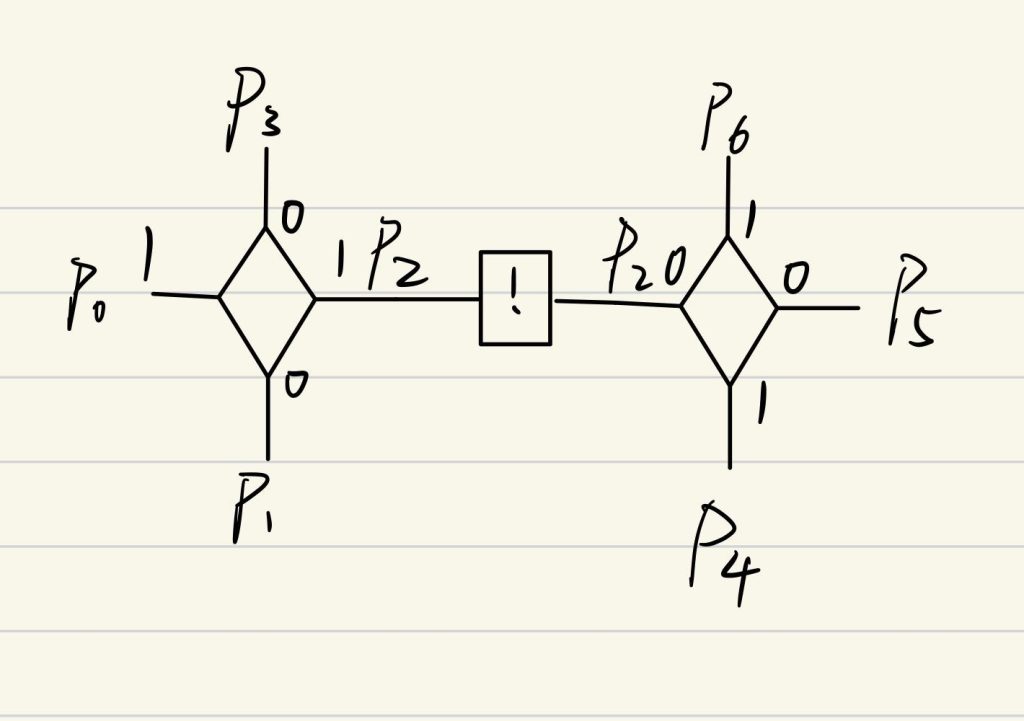
我们先用三个元件分别代表xyz;假设三条语句c1=(x∨¬y∨z),c2=(¬x∨y∨z),c3=(x∨y∨¬z)我们可以为每条语句分配一个b-g对(下面的三个),然后用线与对应的引脚相连,可以得到下图的电路
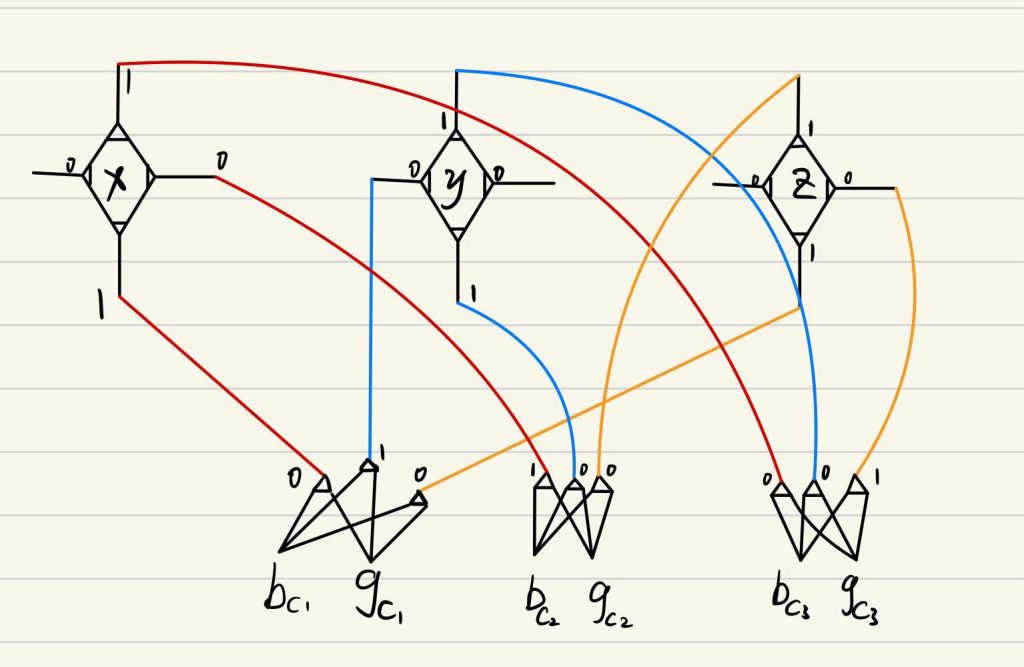
得到电路图之后,我们给x下方的引脚连接高电平,因为每条线上都有一个非门的结构,所以每条线两端都是0和1,很幸运,我们得到了一组解,这组解是(x,y,z)=(F,F,F)
奇怪,为什么仅仅指派x=F便推出了(x,y,z)=(F,F,F),(x,y,z)=(F,T,T)明明也是一组解,为什么没有被解出来?为什么呢?因为这条电路是错的!
在上面的电路中,我们只能解出一条语句中仅包含一个为真指派的情况,所以我们需要一些多余的b-g对来存储这些多余的1,需要多少个呢?
我们用了3个元件,每个元件由4个pet,所以我们至少需要12个b-g对;现在元件中有3*2个b-g对,3个语句对应3个b-g对,所以我们还需要3个b-g对,将这些b-g对与每个pet都相连,使其能够恰好吸纳多余的1,我们也意外地得到了3-SAT规约到的特殊3D匹配问题。
如果我们让上面那一段变得抽象些,假设3-SAT问题含n个字句,m个变量,则我们需要补充的b-g对是4n-2n-m=2n-m个
3D匹配→0/1方程组ZOE
没讲
0/1方程组ZOE→子集和
0/1方程组→整数线性规划ILP
0/1方程组→汉密尔顿环
懒得看
汉密尔顿环→旅行商人问题TSP
给定一个汉密尔顿环问题的图G,因为TSP问题需要完全图,所以将图补全,原来的边权值设为1,补充的边权值设为1+k,跑一遍TSP,看权值是否为|V|
任意问题→SAT
任意问题通过程序都可以表示成SAT(电脑作为介质)
应对NP-完全问题
尽管很难,但我们希望能做些什么
近似算法
首先定义近似比:
对于最小化问题,近似比为
对于最大化问题,近似比为
集合覆盖
讲过,显然没记住
我们每次选取一个新的集合,都至少会包含a/OPT个新元素,a为未被找到的元素的个数,也就有
应用1-x≤e-x
可以得到at=0时t=ln n·OPT,n为元素个数
此算法的近似比为ln n
顶点覆盖、最大匹配
最大匹配:在图中找出不包含相同顶点的n个边,使n最大
最大匹配的贪婪算法(极大匹配算法):不断地找两个顶点都未被覆盖的边,并加入集合
顶点覆盖的贪婪算法:选取极大匹配的边的顶点
顶点覆盖贪婪算法的近似比:2
proof:显然,对于任意一个匹配(无论最大或极大),n≤OPT(选择的n条边至少需要n个顶点来覆盖)
k-簇问题
问题描述:将平面上的点用k个圆包含进去,使最大圆的半径最小
贪婪算法:把圆心放在几何中心,但是任意坏
近似算法:
- 随机找到一个顶点A,然后找到一个距离A最远的顶点B…直到找到k个顶点,
- 将这k个顶点作为圆心
近似比为2
proof:

假设我们近似算法得到的圆心为ABCD,而B对应的最优解是B’,r≤a+b≤2R,R为最优值
旅行商人问题TSP
我们需要一条现实中存在的路径,在地图上存在的路径,否则改近似算法不可用
近似算法:
- 算出最小生成树
- 补出蓝色路径(欧拉回路)
- 沿蓝色路径走,如果访问过就跳到下一个节点
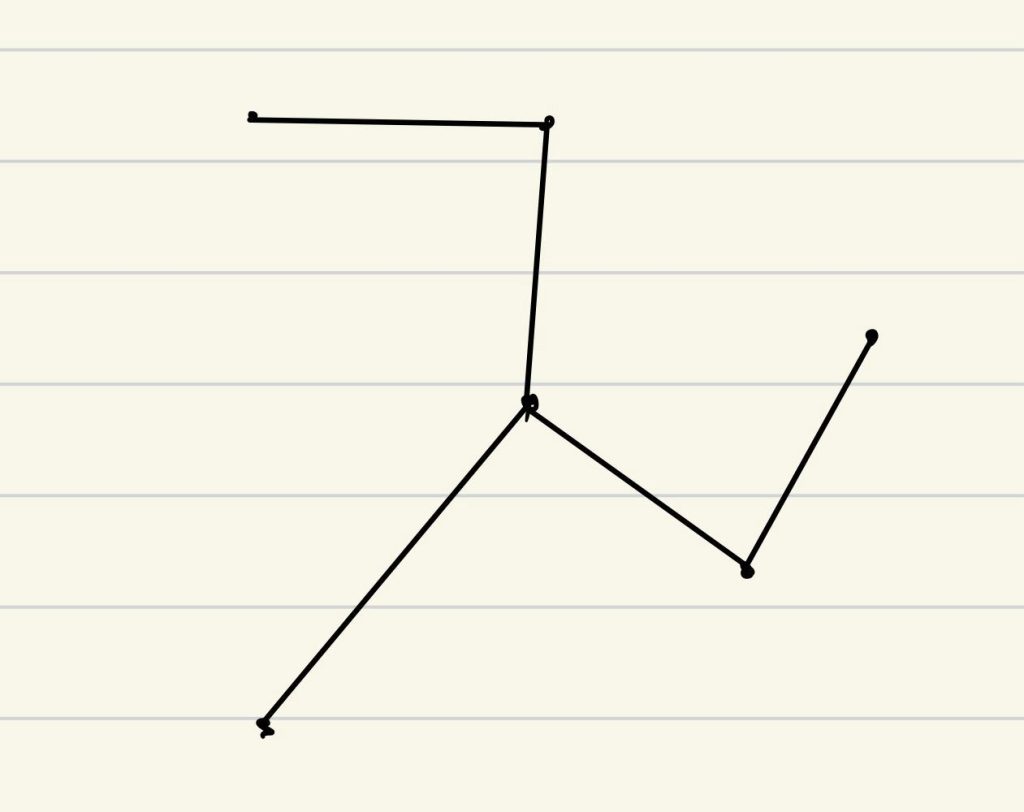


近似比为2
proof:MST≤OPT & Red_Path ≤2*MST=Blue_Path
更好的算法:“double edge”过于粗暴
- 我们挑出奇数度的顶点
- 将顶点配对后连接,同样可以得到一个欧拉回路(这里需要用最小的边连接,这个问题不难)
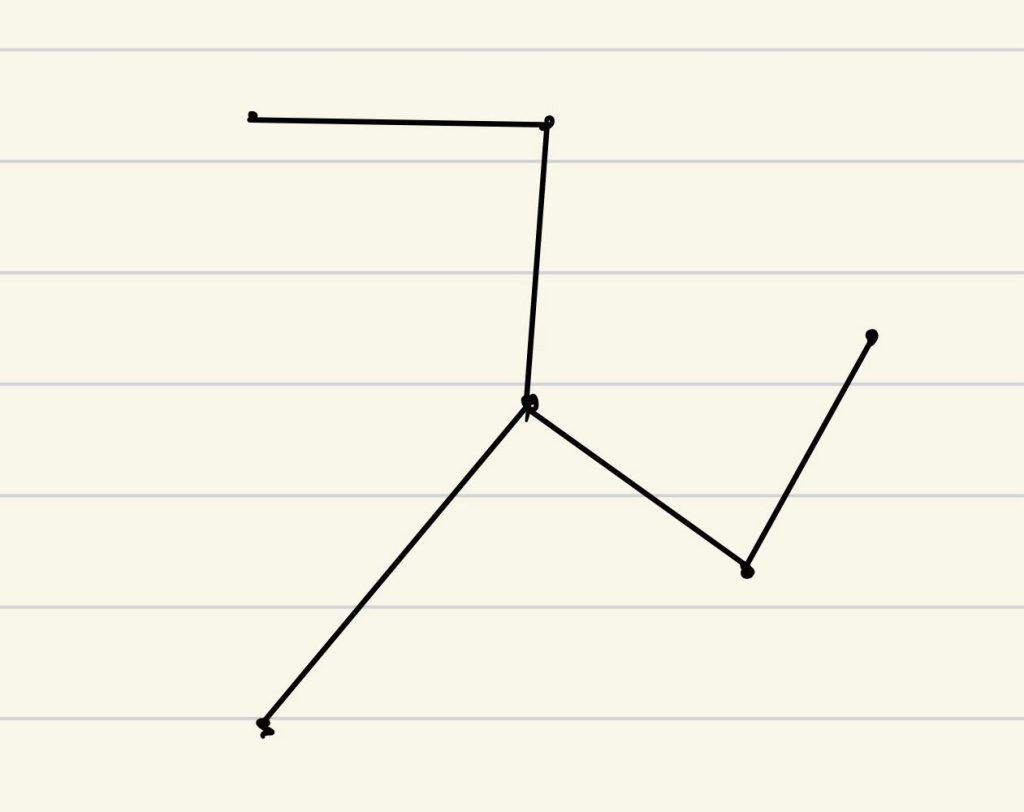
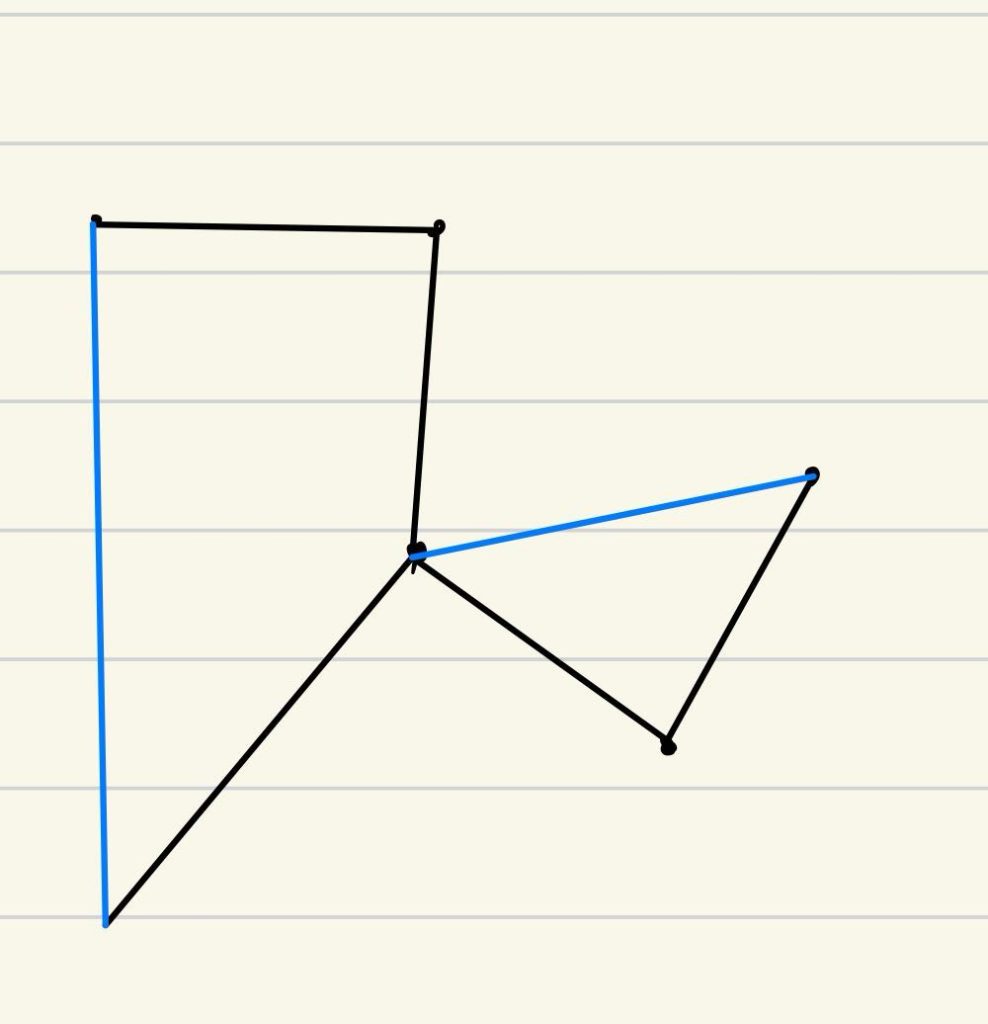

近似比1.5
proof:Blue_Path+Yellow_Path≤OPT,因为Blue_Path≤Yellow_Path,所以Blue_Path≤1/2OPT
Blue_Path+MST≤3/2OPT
背包问题
比较特殊,给定一个ε,我们可以得到一个近似度为1+ε的解,越接近1,算法复杂度越大
另外,除了之前讲过的O(nW)的算法,我们还有一个O(nV)的算法
算法:
- vmax为最高的价值
- 令vi‘=⌊vi·n/ε·vmax⌋,n为元素个数(将V的位数变小了,当然也带来了一些误差,实际上就是忽略后几位,只比较前几位)
- 使用vi‘运行动态规划
得到的vi‘最大为n/ε,应用O(nV)的算法,时间复杂度为O(n3/ε)
近似比?
令S为原问题精确解的集合,K*为最优值;S’为得到的近似解,则有
近似算法总结
NP-完全问题和近似算法可以分成几类
- 旅行商人问题没有近似算法
- 顶点覆盖、k-簇、地图上的旅行商人问题有近似度有限的近似算法
- 背包问题有出错率接近于0的近似算法
- 集合覆盖问题有近似度log n的近似算法
回溯(不考)
从SAT到CNF——Tseitin Encoding
一般的逻辑表达式化成一个CNF需要指数级时间,所以我们不想化成一个严格等价的式子,可满足性等价即可
一般算法:
CNF(ф){
case
| · ф is a literal: return ф
| · ф is φ1 ∧ φ2: return CNF(φ1)^CNF(φ2)
| · φ is φ1 ∨ φ2: return Dist(CNF(φ1),CNF(φ2))
}
Dist(φ1, φ2){
case
| · φ1 is ψ11 ^ ψ12: return Dist(ψ11,φ2)^ Dist(ψ12,φ2)
| · φ2 is ψ21 ^ ψ22: return Dist(φ1,ψ21)^ Dist(φ1, ψ22)
}
Tseitin Encoding:
假设原式(A→(B∧C)),构建一颗树,在每个非叶结点上添加一个新变量
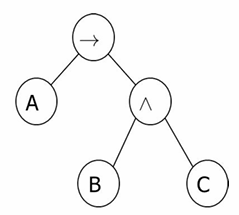
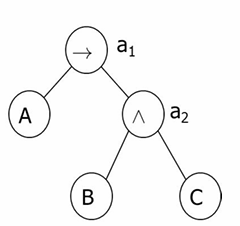
通过右图我们可以得到一个新的式子(a1↔(A→a2))∧(a2↔(B∧C))∧(a1),进而写出CNF
因为Tseitin Encoding避免了两个大式子取或,所以难度降低
回溯
解SAT问题的过程:
- 给定一个变量的指派,对于每条语句,如果被满足则把语句删除;否则将此变量删去
- 对于某个语句,结果是被删除(被满足)或者出现空括号(不可被满足)
- 如果所有指派都出现空括号,则不可被满足
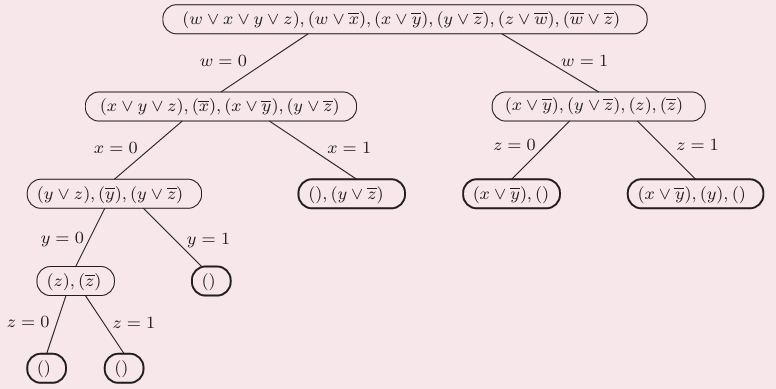
在一个大式子中,我们不能尝试每种指派,所以我们需要记住一些中间结果(比如令x=0后,只有一种yz的取值能使式子可满足,那么我们需要直接赋值yz)。在应用这些中间结果后,我们需要在回溯时将其一并回溯。
algo:
SAT()
while true do
| if ¬Decide() then
| | return true ;
| end
| else
| | while ¬BCP() do
| | | if ¬Resolve-conflict() then return false;
| | end
| end
end- Decide(): Choose the next variable and value. Return False if all variables are assigned.
- BCP(): Apply repeatedly the unit clause rule. Return False if reached a conflict.
- Resolve-conflict(): Backtrack until no conflict. Return False if impossible.
冲突语句
我们用x1=0@4表示变量x1在第四轮指派中被置为0,在推理过程中我们得到了下面这样的结果,K表示发生冲突,实心点是指派,空心点是通过推理推出的结果
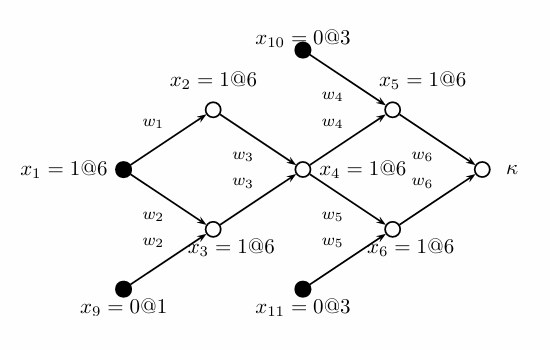
那么我们可以很自然地得到一条新的语句(称为冲突语句),(¬x1∨x9∨x11∨x10),然后回溯到最后一个指派(x1=1@6),我们重新将x1置0,然后再进行推理,再学习新的语句
但每个冲突我们只能学到一条语句吗,显然不是
(¬x1∨x9∨x11∨x10)
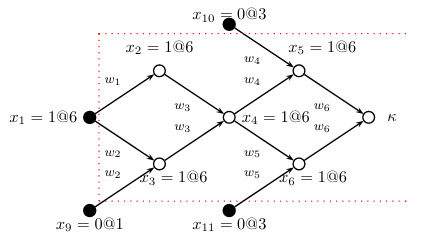
(¬x4∨x11∨x10)
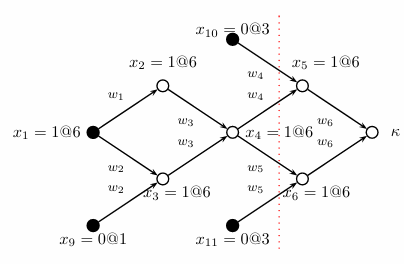
(¬x2∨¬x3∨x11∨x10)
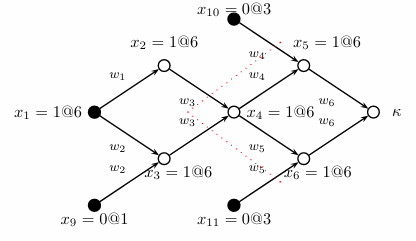
我们将树任意切割,都可以得到新的冲突语句,所以我们学习的原则应该是什么?
——目前的求解器大多使用第一种
CDCL
如果在第6层的指派上出现了冲突,之前我们会对第6层重新赋值,但我们还可以跳过这一过程(因为很容易还得到冲突),直接回溯到更高一层,也确实得到更好的性能
局部搜索(不考)

梯度下降-顶点覆盖
算法:
- 将所有顶点放入S集合
- 定义“邻居”:和S仅有增加/减少1个顶点的区别
- 如果S有一个邻居S’比S更优,S=S’
- 重复第三步
算法复杂度:O(|V|),因为最多可以减去O(|V|)个顶点
算法结果任意差
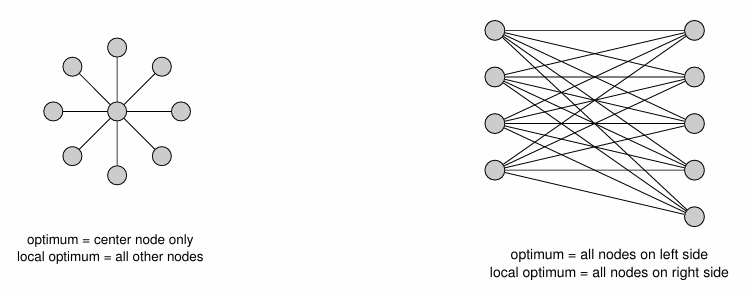
旅行商人问题TSP
2-Change Neighborhood
因为是完全图,所以可以任意找到一个经过所有订单的环,因为不可能只换一条边,所以我们找两条边做如下交换

每个解的邻居有|V2|个,且替换可能有指数级的次数,所以我们尝试将“邻居”的个数增加,以尽可能减少替换的次数
3-Change Neighborhood
将邻居的定义修改成替换2-3条边,邻居的个数增加到|V3|,替换的次数有所减少,但我们不能一再增加邻居的个数
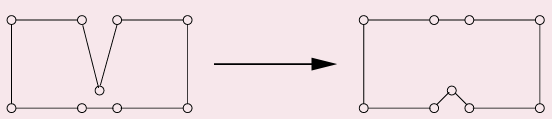
图分割
问题描述:将图分为两部分,每部分的顶点不小于α|V|,0<α≤0.5,最小化“割”的权值
大都市算法
我们能否“跳出”局部最优解,来得到整体最优解
吉布斯-玻尔兹曼函数
一个物体在能量为E、温度为T时处于稳态的概率如下,k为常数
T越高,能量高的稳态和能量低的稳态概率差距越小;反之越大
算法:
- 给定一个固定温度T,初始状态S
- 找到一个邻居S’
- 如果S’更优,则S=S’
- 如果S更优,有e-ΔE/(kT)的概率令S=S’
这样虽然可以达到全局最优,但是不容易终止
想法:T随程序运行而降低,注意控制速度。降温太快很难达到最优值,降温太慢算法太慢
Hopfield神经网络
问题描述:
- 输入:无向图G,边有正负整数权值
- 我们需要将顶点v标记成1或-1,记为sv
- 定义“Good Edge” e(u,v):susvwe<0
- 定义“Satisfied Node” v:与v相连的边中Good Edge的数量大于Bad Edge
- 输出:所有顶点v都是Satisfied Node的一个sv的指派
状态反转算法
如果一个顶点的bad edge大于good edge,则将该点的指派取反
HOPFIELD-FLIP(G, w)
S ←arbitrary configuration;
while current configuration is not stable do
| u ←unsatisfied node;
| su ←−su;
end
return S不断反转会不会不终止?
——不会,因为每次反转都会让satisfied node变多,且有上界
最大割
权值为正的无向图,类似最小割问题,以最大的一个割将图分割成两部分
可以归约到上面的Hopfield神经网络问题,即在边权值为正的情况下。
贪婪算法
也可以用下面的贪婪算法解,对一个顶点v,将其放在能使割最大的集合中:
MAX-CUT-LOCAL(G, w)
while there exists an improving node v do
| if v ∉ A then
| | A←A∪{v};B ←B−{v};
| end
| else
| | B ←B∪{v};A←A−{v};
| end
end
return(A,B)是一个近似比为2的近似算法,因为每次选择都会选择一部分边、抛弃一部分边,选择的比抛弃的权值大;但是不是多项式时间的算法
Big-improvement-flip 算法
将顶点flip时,强制要求增加的权值大于等于2ε/n*w(A,B),最终近似比为1/(2+ε)
为什么是多项式时间算法:
KL-neighborhood
总结
7道题。
建模、证明、算法分析20‘:含应用题
算法策略30’
- DFS、BFS
- 最短路径,MST
- DAG上的算法
- 模运算
- 网络流
证明NPC问题15’
- 证明NPC:规约+证明是NP 15’
处理NP-Hard问题10‘
- 近似算法(和课上的四个很类似,那可能没有集合覆盖) 10‘
回溯局部最优
